Tilføjelse og fradrag af brøker er en vigtig færdighed at have. Brøker dukker op i dagligdagen hele tiden, især i matematikundervisning, fra elementær til college. Følg disse trin for at lære at tilføje og fratrække brøker fra ækvivalente brøker, ulige brøker, blandede tal eller almindelige brøker. Hvis du allerede kender en måde, er det virkelig let at løse de andre fraktioner!
Trin
Metode 1 af 4: Tilføjelse og subtraktion af brøker med samme nævner
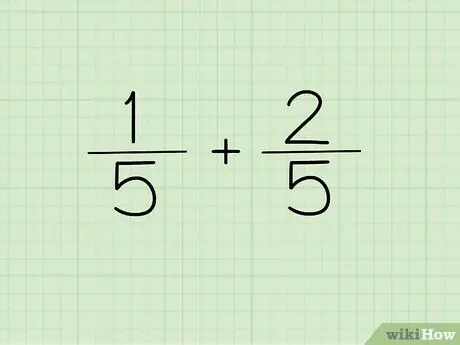
Trin 1. Skriv dit spørgsmål ned
Hvis nævneren for de to brøker, du vil tilføje eller trække fra, er den samme, skal du skrive nævneren én gang som nævner for dit svar.
Med andre ord behøver 1/5 og 2/5 ikke at skrives som 1/5 + 2/5 =?, men kan skrives som (1+2)/5 =?. Nævnerne er de samme, så de kan kun skrives én gang. De to tællere kombineres
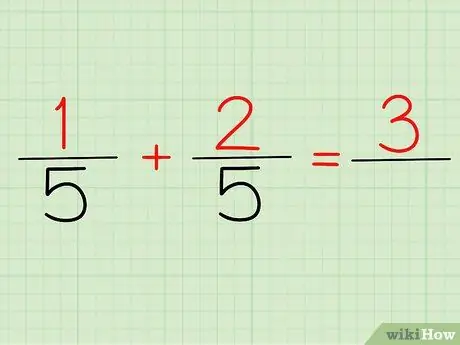
Trin 2. Tilføj tællerne
Tælleren er det tal, der er over enhver brøk. Hvis vi ser på problemet ovenfor, er 1/5 og 2/5, 1 og 2 vores tællere.
Uanset om du skriver det 1/5 + 2/5 eller (1 + 2)/5, vil dit svar være det samme: 3! Fordi 1 + 2 = 3

Trin 3. Forlad nævneren
Da nævnerne er de samme, skal du ikke gøre noget med nævnerne! Tilføj ikke, træk, multiplicér eller divider. Lad det være.
Så fra det samme eksempel er vores nævner 5. Right! 5 er det nederste tal i vores brøk. Vi har det halve svar

Trin 4. Skriv dit svar ned
Det eneste du skal gøre er at skrive din tæller og nævner ned! Hvis du bruger eksemplet ovenfor, er dit svar 3/5.
Hvad er din tæller? 3. Din nævner? 5. Derfor er 1/5 + 2/5 eller (1 + 2)/5 lig med 3/5.
Metode 2 af 4: Tilføjelse og subtraktion af brøker med forskellige nævnere

Trin 1. Find den mindst fællesnævner
Det vil sige, at den mindste nævner er den samme for begge brøker. Antag, at vi har fraktionerne 2/3 og 3/4. Hvad er nævneren? 3 og 4. For at finde den mindst fællesnævner for begge brøker kan du gøre dette på tre måder:
- Skriv multiplerne af. Multipler af 3 er 3, 6, 9, 12, 15, 18 … og så videre. Multipler på 4? 4, 8, 12, 16, 20 og så videre. Hvad er det mindste tal, der er et multiplum af de to? 12! Det er den mindst fællesnævner.
-
Primær faktorisering. Hvis du kender til faktorer, kan du udføre primfaktorisering. Det vil sige, at du leder efter de tal, der udgør din nævner. For tallet 3 er faktorerne 3 og 1. For tallet 4 er faktorerne 2 og 2. Derefter alle sammen. 3 x 2 x 2 = 12. Din mindst fællesnævner!
Gang alle tallene for det mindre tal. I nogle problemer, som denne, kan du gange begge tal - 3 x 4 = 12. Men hvis du har en stor nævner, skal du ikke gøre dette! Du vil ikke gange 56 x 44 og gå helt ud for at få 2.464

Trin 2. Multiplicer nævneren med det antal, der er nødvendigt for at få den mindste fællesnævner
Med andre ord vil du have, at alle dine nævnere er lige. I vores eksempel ønsker vi, at nævneren er 12. For at ændre 3 til 12, multiplicerer du 3 med 4. For at ændre 4 til 12, multiplicerer du 4 med 3. Den samme nævner vil være nævneren for dit endelige svar.
-
Så 2/3 bliver 2/3 x 4 og 3/4 bliver 3/4 x 3. Det vil sige, at vi nu har 2/12 og 3/12. Men vi er ikke færdige endnu!
- Du vil bemærke, at nævnerne ganges med hinanden. Dette kan gøres i denne situation, men ikke i alle situationer. Nogle gange, i stedet for at gange begge nævnere, kan du gange begge nævnere med et andet tal for at få det mindre tal.
- I andre problemer skal du nogle gange bare gange den ene nævner for at gøre den lig med nævneren for den anden brøkdel i problemet.

Trin 3. Multiplicer tælleren med det samme tal
Når du gange nævneren med et tal, skal du også gange tælleren med det samme tal. Det, vi gjorde i det sidste trin, er kun en del af multiplikationen, der skal udføres.
Vi har 2/3x4 og 2/4x3 som det første trin - derefter, i det andet trin, 2 x 4/3 x 4 og 3 x 3/4 x 3. Det vil sige, at vores nye tal er 8/12 og 9/ 12. Perfekt
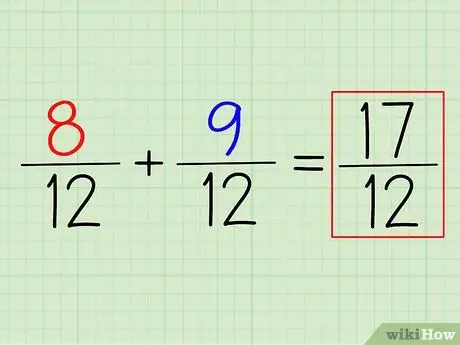
Trin 4. Tilføj (eller træk) tællerne for at få svaret
For at tilføje 8/12 + 9/12 skal du blot tilføje tællerne. Husk: bare lad nævneren stå. Den mindste nævner, du finder, er din sidste nævner.
I dette eksempel (8+9)/12 = 17/12. For at konvertere det til et blandet tal skal du blot trække nævneren fra tælleren og skrive resten ned. I dette tilfælde er 17/12 = 1 5/12
Metode 3 af 4: Tilføjelse og subtraktion af blandede og almindelige fraktioner
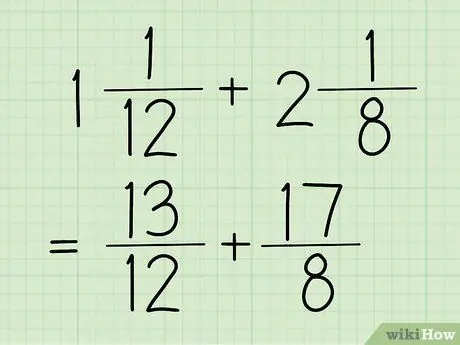
Trin 1. Konverter dine blandede fraktioner til almindelige brøker
Et blandet tal er en brøk, der har et helt tal og en brøk, som i eksemplet ovenfor (1 5/12). I mellemtiden er en almindelig brøkdel en brøkdel, hvis tæller (øverste tal) er større end nævneren (nederste tal). Denne brøkdel ses også i det foregående trin, som er 17/12.
For eksemplerne i dette afsnit vil vi bruge 13/12 og 17/8

Trin 2. Find en fællesnævner
Kan du huske de tre måder at finde den mindst fællesnævner på? Ved at skrive multipler, bruge primfaktorisering eller multiplicere nævnerne.
Lad os finde multipler af vores eksempel, 12 og 8. Hvad er det mindste tal, som de begge har til fælles? 24. 8, 16, 24 og 12, 24 - bingo

Trin 3. Multiplicer din tæller og nævner for at finde den tilsvarende brøk
Begge nævnere skal ændres til 24. Hvordan konverterer man 12 til 24? Gang med 2. 8 til 24? Gang med tre. Men glem ikke - du skal også gange tællerne!
Så (13 x 2)/(12 x 2) = 26/24. Og (17 x 3)/(8 x 3) = 51/24. Vi er næsten færdige med dette

Trin 4. Tilføj eller træk dine fraktioner
Nu hvor du har den samme nævner, kan du nemt tilføje de to tællere sammen. Husk, bare lad nævneren være!
26/24 + 51/24 = 77/24. Det er din sum! Tallene i toppen var dog for store …

Trin 5. Konverter dit svar tilbage til blandede tal
Det meget store tal øverst i brøken føles lidt underligt - du kan ikke se størrelsen på din brøk. Alt du skal gøre er at trække din nævner fra tælleren gentagne gange, indtil den ikke kan trækkes yderligere og skrive resten ned.
-
I dette eksempel 77 minus 24 gange 3 gange. Det vil sige 24 x 3 = 72. Resten er 5! Så hvad er dit slutresultat? 3 5/24.
Så sandt!
Metode 4 af 4: Tilføj og træk fraktioner uden at finde LCM
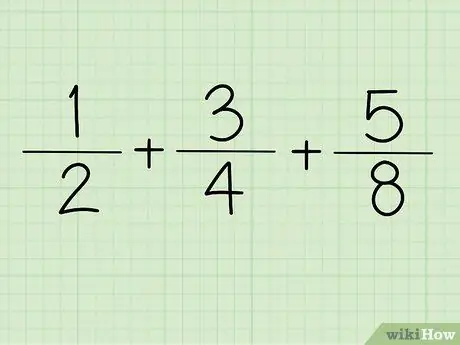
Trin 1. Skriv brøkdelen ned
For eksempel + +

Trin 2. Løs tælleren først
- Gang med den anden brøk tæller.
- Gang 1 med 4 og 8. [32]
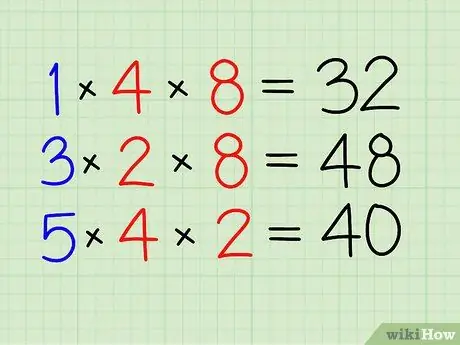
Trin 3. Gør det samme for de andre fraktioner
- Gang 3 med 2 og 8. [48]
- Til sidst multipliceres 5 med 4 og 2. [40]
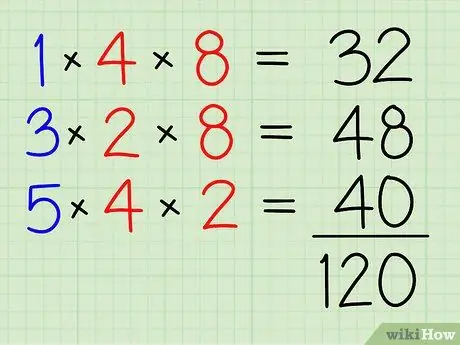
Trin 4. Tilføj dem alle sammen
32+48+40=120
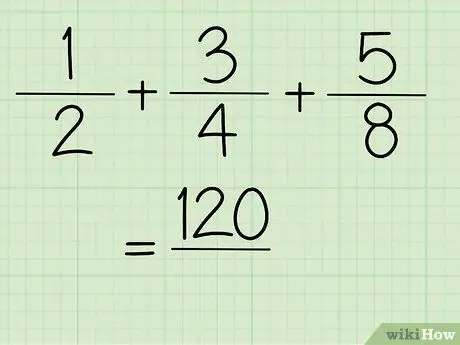
Trin 5. Nu får du tællerværdien

Trin 6. Løs brøkerens nævner

Trin 7. Multiplicer alle fraktionernes nævnere
2×4×8=64

Trin 8. Nu får du resultatet
120/64 = 1 56/64 = 1 ⅞
Advarsel
- Denne metode giver dig mulighed for at multiplicere store tal.
- Du skal muligvis bruge en lommeregner til at beregne denne måde.







