At dele en brøkdel med en brøkdel kan virke forvirrende i starten, men det er faktisk virkelig let. Alt du skal gøre er at vende, formere og forenkle! Denne artikel vil guide dig gennem processen og vise dig, hvor let det er at dele en brøkdel med en brøkdel.
Trin
Del 1 af 2: Forståelse for hvordan man deler brøker med brøker
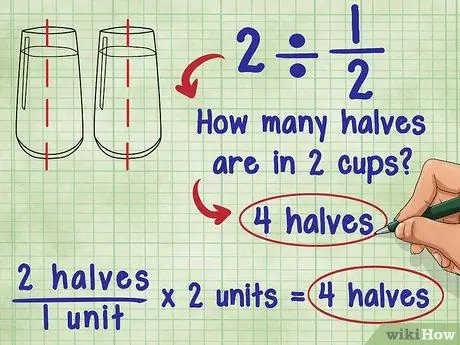
Trin 1. Tænk over, hvad dividering med en brøkdel betyder
Om 2 ÷ 1/2 spurgte Ada: "Hvor mange halvdele er i 2?" Svaret er 4, fordi hver enhed (1) består af to "halv", og der er 2 enheder i alt: 2 "halv"/1 enhed * 2 enheder = 4 "halv".
- Prøv at forestille dig den samme ligning ved hjælp af et glas vand: Hvor mange et halvt glas vand er i 2 glas vand? Du kan hælde 2 og en halv kopper vand i hvert glas vand. Det betyder, at du i bund og grund tilføjer de "halve" glas vand, og du har to glas: 2 "halv"/1 kop * 2 kopper = 4 "halv".
- Det betyder, at hvis den brøkdel, du deler, er mellem 0 og 1, er svaret altid større end det originale tal! Dette er sandt, når du dividerer et helt tal eller brøk med en brøk.

Trin 2. Forstå, at dividering er det modsatte af at multiplicere
Således kan dividere med en brøkdel løses ved at gange med fraktionens reciprokke. Det gensidige af en brøk (også kaldet "multiplikationsinversen") er den brøkdel, der er inverteret, så tæller og nævner bytter plads. På et øjeblik deler vi brøker med brøker ved at finde den anden fraktors reciprokke og multiplicere begge brøker. Lad os dog først se på nogle af modsætningerne:
- Det gensidige af 3/4 er 4/3.
- Det modsatte af 7/5 er 5/7.
- Det gensidige af 1/2 er 2/1 eller 2.
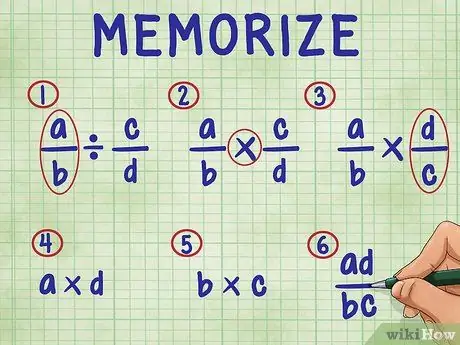
Trin 3. Husk følgende trin for at dividere en brøk med en brøk
For at rækkefølgen omfatter trinene:
- Bare lad den første brøk i ligningen.
- Skift divisionstegnet til multiplikationstegnet.
- Vend den anden fraktion (find dens gensidige).
- Gang tælleren (øverste tal) af begge brøker. Multiplikationsresultatet er tælleren (øverst) på dit svar.
- Multiplicer nævneren (bundnummer) for begge brøker. Produktet af produktet er nævneren for dit svar.
- Forenkle dine brøker ved at forenkle dem til deres enkleste vilkår.
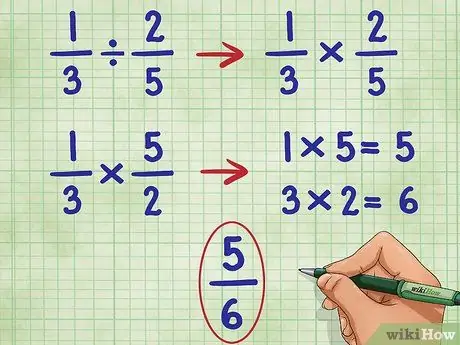
Trin 4. Udfør disse trin for 1/3 2/5 eksemplet
Vi starter med at udelade den første brøkdel og konvertere divisionstegnet til multiplikationstegnet:
- 1/3 ÷ 2/5 = Bliver til:
- 1/3 * _ =
- Nu vender vi den anden brøk (2/5) for at finde dens gensidige, som er 5/2:
- 1/3 * 5/2 =
- Nu multiplicerer tælleren (øverste tal) for begge brøker, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Nu multipliceres nævneren (bundnummer) for begge brøker, 3*2 = 6.
- Nu har vi: 1/3 * 5/2 = 5/6
- Denne brøkdel kan ikke forenkles yderligere, så vi har vores svar.

Trin 5. Prøv at huske følgende rim for at hjælpe dig med at huske:
"Opdeling af brøker er let, vend den anden fraktion om og multiplicér derefter. Glem ikke at forenkle, før det er tid til at spise."
En anden nyttig påmindelseshjælp fortæller dig, hvad du skal gøre med hver del af ligningen: "Lad mig (første brøk), Skift mig (divisionstegn), Vend mig om (anden brøk)."
Del 2 af 2: Opdeling af brøker efter brøker i problemer
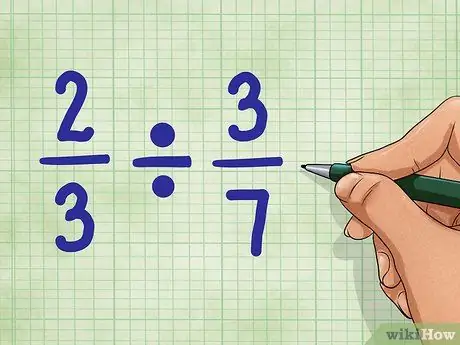
Trin 1. Start med eksempler på spørgsmål
Lad os bruge 2/3 ÷ 3/7. Dette spørgsmål beder om antallet af dele svarende til 3/7, som kan findes i værdien 2/3. Vær ikke urolig. Det er ikke så svært som det lyder!
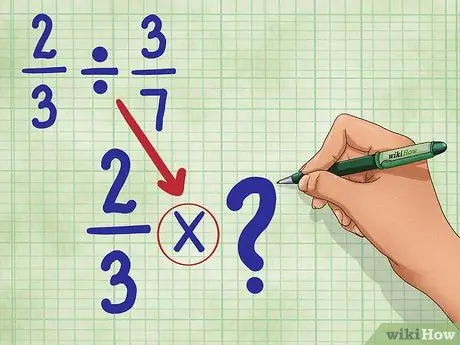
Trin 2. Konverter divisionstegnet til multiplikationstegnet
Din nye ligning vil være: 2/3 * _ (Vi udfylder dette emne om et øjeblik.)
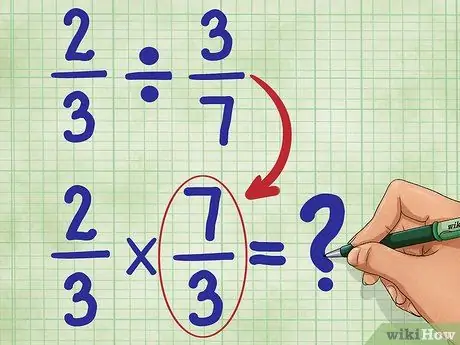
Trin 3. Find nu det gensidige af den anden brøk
Det betyder at vippe 3/7, så tælleren (3) nu er i bunden, og nævneren (7) nu er øverst. Det gensidige af 3/7 er 7/3. Skriv nu din nye ligning:
2/3 * 7/3 = _

Trin 4. Gang dine brøker
Gang først tællerne for begge brøker: 2 * 7 = 14. 14 er tælleren (øverste nummer) for dit svar. Multiplicer derefter nævnerne for begge brøker: 3 * 3 = 9. 9 er nævneren (bundnummer) for dit svar. Nu ved du det 2/3 * 7/3 = 14/9.
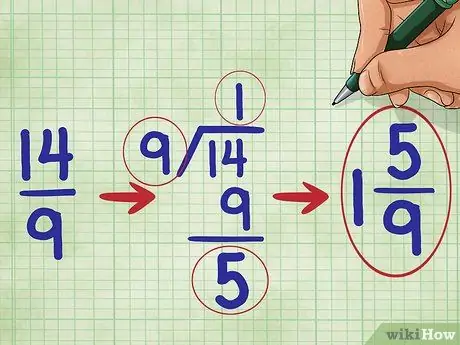
Trin 5. Forenkle din brøkdel
I dette problem, fordi tælleren af brøken er større end nævneren, ved vi, at vores brøk er større end 1. Vi skal konvertere den til et blandet tal. (Et blandet tal er et helt tal og en brøk sammenlagt, f.eks. 1 2/3.))
-
Del først tælleren
Trin 14. med 9.
Tallet 14 divideret med 9 er lig med et med en rest på 5, så du bør skrive din forenklede brøk ned som: 1 5/9 ("En fem-nineth").
- Stop, du har fundet svaret! Du kan angive, at du ikke længere kan forenkle brøken, fordi nævneren ikke er delelig med tælleren (9 er ikke delelig med 5), og tælleren er et primtal eller et heltal, der kun er delbart med en og selve tallet.
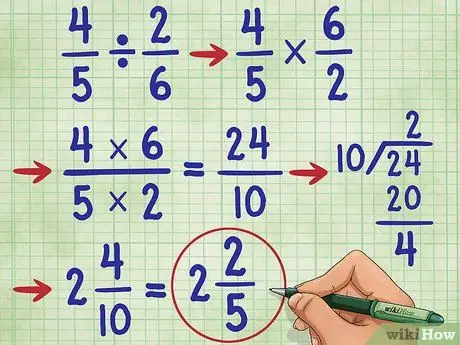
Trin 6. Prøv et andet eksempel
Lad os prøve spørgsmålet 4/5 ÷ 2/6 =. Først skal du ændre divisionstegnet til multiplikationstegnet (4/5 * _ =), så find det gensidige af 2/6, hvilket er 6/2. Nu har du ligningen: 4/5 * 6/2 =_. Nu skal du gange tælleren, 4 * 6 = 24, og nævneren 5* 2 = 10. Nu har du 4/5 * 6/2 = 24/10.
Forenkle nu brøken. Da tælleren er større end nævneren, skal vi konvertere denne brøk til et blandet tal.
- Divider først tælleren med nævneren, (24/10 = 2 resterende 4).
- Skriv svaret som 2 4/10. Vi kan stadig forenkle denne brøkdel igen!
- Bemærk, at 4 og 10 er lige tal. Så det første trin til at forenkle det er at dividere hvert tal med 2. Vi får 2/5.
- Da nævneren (5) ikke er delelig med tælleren (2) og 5 er et primtal, ved vi, at denne brøkdel ikke kan forenkles yderligere. Så vores svar er: 2 2/5.

Trin 7. Få yderligere hjælp til at forenkle brøker
Du har sandsynligvis brugt meget tid på at lære at forenkle brøker, før du prøver at dele dem med hinanden. Men hvis du har brug for en opdatering eller anden hjælp, er der nogle gode onlineartikler, der kan være en stor hjælp for dig.
Relaterede wikiHow -artikler
- Konvertering af almindelige brøker til decimaler
- Beregning af en cirkels areal
- Opdeling af polynomer ved hjælp af syntetisk division
- Deling af blandede fraktioner







