Du tror måske, at heltal bare er almindelige tal, som 3, -12, 17, 0, 7000 eller -582. Heltal kaldes også hele tal, fordi de ikke er opdelt i dele som brøker og decimaler. Læs denne artikel for at lære alt, hvad du har brug for om at tilføje og fratrække heltal, eller læs direkte det afsnit, du har brug for.
Trin
Metode 1 af 5: Tilføjelse og subtraktion af positive heltal ved hjælp af en talelinje

Trin 1. Forstå tallelinjen
Talelinjer gør grundlæggende matematik til noget håndgribeligt og fysisk, som du kan se. Med blot et par tegn og sund fornuft kan vi bruge det som en lommeregner til at tilføje og trække tal.

Trin 2. Tegn en basisnummerlinje
Forestil dig eller tegn en lige lige linje. Lav en prik i midten af din linje. Skrive 0 eller nul ved siden af denne periode.
Din matematikbog kalder dette måske udgangspunktet, fordi det er udgangspunktet for alle tal

Trin 3. Tegn to prikker, en hver til højre og venstre for dit nul
Skrive - 1 ved siden af prikken til venstre og
Trin 1. ved siden af prikken til højre. Dette er heltalet tættest på nul.
- Du skal ikke bekymre dig om at gøre afstandene mellem punkterne nøjagtig de samme - så længe du ved, hvad hvert punkt betyder, kan der bruges en talelinje.
- Venstre side er begyndelsen på sætningen.

Trin 4. Fuldfør din tallinje ved at tilføje flere tal
Lav flere prikker til venstre end -1 og til højre end 1. Til venstre, fra -1, markér dine prikker med - 2, - 3, og - 4. Til højre, fra 1, markér din prik med
Trin 2
Trin 3., da
Trin 4.. Du kan fortsætte, hvis du har plads på dit papir.
Eksemplet i figuren viser en talelinje fra -6 til 6

Trin 5. Forstå positive og negative heltal
Positive heltal, også kaldet naturligt tal, er et helt tal større end nul. 1, 2, 3, 25, 99 og 2007 er positive heltal. Negative heltal er heltal, der er mindre end nul (f.eks. -2, -4 og -88).
Heltal er en anden måde at kalde hele tal på. Brøker som 1/2 (halvdelen) er kun en del af tallet, så de er ikke heltal. Samme som decimal, f.eks. 0,25 (nulpunkt to fem); decimal er ikke et heltal

Trin 6. Start med at løse 1+2 ved at placere din finger på punkt 1
Vi løser simple tilføjelsesproblemer 1+2 ved hjælp af den talelinje, du lige har oprettet. Det første tal er
Trin 1., så begynd at sætte din finger på nummeret.
-
Er dette spørgsmål for let?
Hvis du nogensinde har tilføjet, kender du sikkert svaret på 1+2. Godt: hvis du kender resultatet, bliver det lettere at forstå, hvordan tallinjen fungerer. Derefter kan du bruge talelinjen til at løse mere vanskelige tilføjelsesproblemer eller forberede dig på vanskeligere matematik som algebra.

Trin 7. Tilføj 1+2 ved at flytte din finger 2 prikker til højre
Skub din finger til højre og tæl antallet af prikker (et andet nummer), du sender. Hvis du har bestået 2 nye point, skal du stoppe. Det nummer, din finger peger på, er svaret,
Trin 3
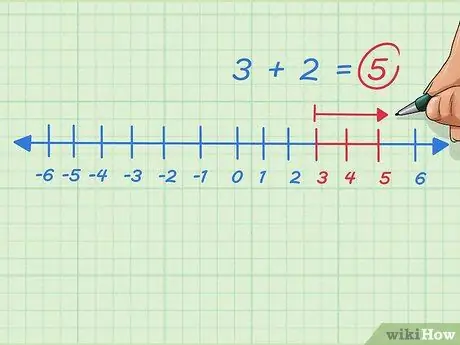
Trin 8. Tilføj eventuelle positive heltal ved at flytte til højre på tallinjen
Antag, at vi vil løse 3+2. Start med 3, flyt til højre eller tilføj 2 prikker. Vi stopper ved 5. Problemet er skrevet 3 + 2 = 5.

Trin 9. Træk positive heltal fra ved at flytte til venstre på tallinjen
For eksempel vil vi løse 6 -4, vi starter ved 6, bevæger os til venstre 4 punkter og stopper ved 2. Dette problem er skrevet 6 - 4 = 2.
Metode 2 af 5: Tilføjelse og subtraktion af negative tal ved hjælp af en talelinje

Trin 1. Lær om talelinjer
Hvis du ikke ved, hvordan du opretter en talelinje, skal du vende tilbage til afsnittet Tilføjelse og subtraktion af positive tal ved hjælp af tallinjer for at lære, hvordan du opretter et.
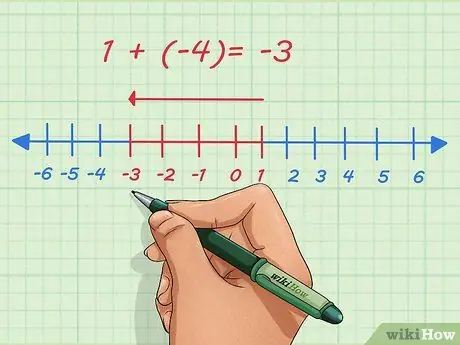
Trin 2. Forstå om negative tal
Positive tal angives med retningen til højre på tallinjen. Negative tal er angivet til venstre på talelinjen. Tilføjelse af negative tal betyder at flytte punktet til venstre på tallinjen.
-
Lad os f.eks. Tilføje 1 og -4. Normalt skrives dette spørgsmål sådan:
1 + (-4)
. På talelinjen starter vi med 1, flytter 4 punkter til venstre og stopper ved -3.
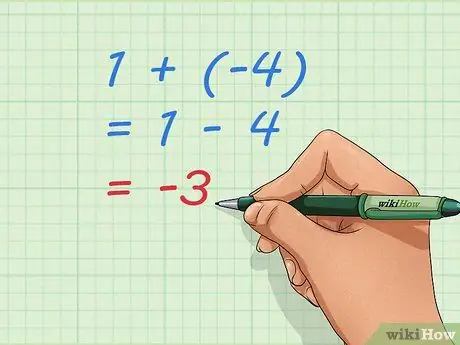
Trin 3. Brug grundlæggende ligninger til at forstå tilføjelsen af negative tal
Bemærk, at -3, vores svar, er det tal, vi får, hvis vi gør 1 -4. At tilføje 1 + (-4) og trække 4 fra 1 er det samme problem. Vi kan skrive det som en ligning, en matematisk sætning, der viser lighed: 1 + (-4) = 1-4 = -3
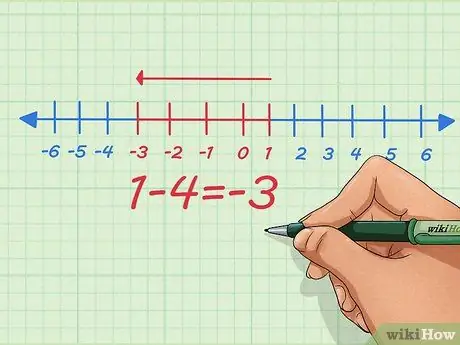
Trin 4. I stedet for at tilføje negative tal, gør det til et subtraktionsproblem ved hjælp af positive tal
Som vi kan se fra den enkle ligning ovenfor, kan vi gøre begge dele - gøre tilføjelsen af negative tal til subtraktion af positive tal og omvendt. Du er måske blevet lært at gøre negativer til negative uden at vide hvorfor - her er hvorfor.
-
For eksempel -4. Når vi tilføjer -4 og 1, trækker vi 1 fra 4. Det kan skrives i matematik ved at skrive
1 + (-4) = 1 - 4
. Vi kan skrive dette på talelinjen, startende ved vores startpunkt ved 1 og derefter tilføje 4 prikker til venstre (med andre ord tilføje -4). Da dette er en ligning, er en ting lig med en anden - så det modsatte er også sandt
1 - 4 = 1 + (-4)
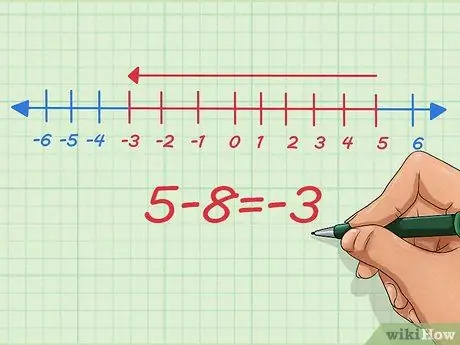
Trin 5. Forstå, hvordan man trækker negative tal fra på en talelinje
På tallinjen er det at fratrække negative tal det samme som at reducere længden. Lad os starte med 5-8.
På tallinjen starter vi ved vores startpunkt ved 5, trækker 8 fra og stopper ved -3
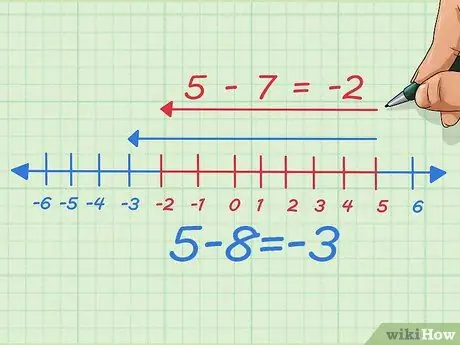
Trin 6. Træk det beløb, du trækker fra, og se, hvad der sker
Antag, at vi trækker en, det tal, vi trækker fra, eller med andre ord trækker 7 i stedet for 8. Nu trækker vi et punkt til venstre på tallinjen. Skriftligt startede vi med 5 - 8 = -3 Nu flytter vi bare 7 til venstre, så det bliver 5 - 7 = -2
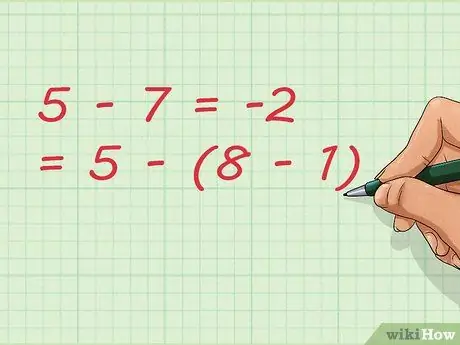
Trin 7. Bemærk, at fratrækning kan resultere i yderligere
I vores eksempel trækker vi tallet 1. Ved at skrive ligningen kan vi skrive det kortere som: 5 - 7 = -2 = 5 - (8 - 1)

Trin 8. Konverter negative tegn til positive, når du tilføjer negative tal
Ved hjælp af trinnet med at konvertere alle subtraktioner til tilføjelser kan vi skrive kortere dem som: 5 - (8 - 1) = 5-7 = 5-8 + 1.
-
Vi ved allerede, at 5 -8 = -3, så tag 5-8 ud af ligningen og indtast -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Vi ved allerede, at 5 -(8 -1) er -trækker et punkt fra 5 -8. Vores ligning kan vise, at 5 -8 er -3, og at trække et punkt fra giver -2. Ligningen kan skrives sådan:
-3 - (-1) = -3 + 1
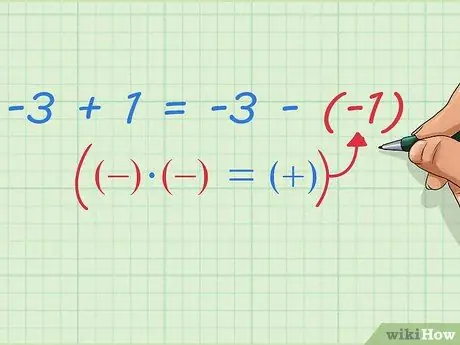
Trin 9. Skriv subtraktion af negative tal som addition
Bemærk hvad der sker efter dette -vi har allerede bevist, at: -3 + 1 = -3 -(-1) Vi kan skrive dette med enklere og mere generelle matematiske regler: første tal plus andet nummer = første tal minus (negativt andet tal) Eller en enklere måde, du sikkert har hørt i matematiklassen: Skift de to negative tegn til et positivt tegn.
Metode 3 af 5: Tilføjelse af positive store heltal

Trin 1. Skriv tilføjelsesproblemet på 2.503 + 7.461 med det ene tal over det andet
Skriv tallene ned i den store kolonne, så 2 er over 7, 5 er over 4 osv. På denne måde lærer vi, hvordan man tilføjer heltal, der er for store til at forestille sig eller bruge talelinjen.
Skriv et + -tegn til venstre for tallet nedenfor og linjen under det, som du måske lærer om mindre tilføjelsesproblemer
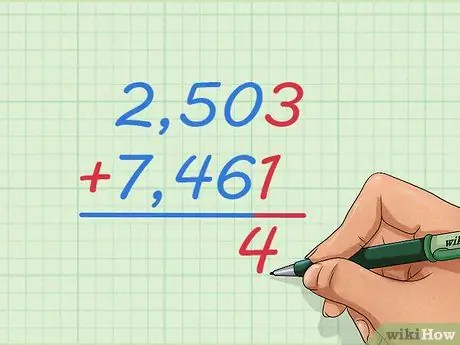
Trin 2. Start med at tilføje de to tal yderst til højre
Det kan være lidt mærkeligt at starte fra højre, fordi vi læser tal fra venstre. Vi skal tilføje fra højre for at få det korrekte svar, som du kan se senere.
-
Under de to tal længst til højre,
Trin 3. da
Trin 1., skriv summen af de to ned
Trin 4..

Trin 3. Tilføj hvert nummer i kolonnen på samme måde
Flyt til venstre, tilføj 0+6, 5+4, og 2+7. Skriv svaret under hvert par numre.
Dit svar skal være: 9.964. Tjek dit arbejde, hvis du laver en fejl.

Trin 4. Tilføj nu 857+135
Du vil bemærke noget andet, så snart du lægger det første par tal til højre sammen. 7+5 er lig med 12, et tocifret tal, men du kan kun skrive et ciffer under den kolonne. Fortsæt med at læse for at finde ud af, hvad du skal gøre, og hvorfor du altid skal starte fra højre og ikke fra venstre.

Trin 5. Tilføj 7+5, og lær, hvor du skal skrive svaret
7+5 = 12, men du kan ikke sætte 1 og 2 under stregen. Men skriv det sidste ciffer ned, Trin 2., under linjen og skriv det første ciffer ned
Trin 1., over kolonnen til venstre, 5+3.
-
Hvis du er nysgerrig efter, hvordan det fungerer, skal du tænke over, hvad opdeling 1 og 2. betyder. Du deler faktisk 12 i
Trin 10. da
Trin 2.. Du kan skrive 10 over tallet, hvis du vil, og du vil se 1 i kolonne 5 og 3, ligesom før.

Trin 6. Tilføj 1+5+3 for at få det næste ciffer i svaret
Nu har du tre cifre at tilføje, fordi du tilføjede 1 til denne kolonne. Svaret er
Trin 9., så dit svar bliver 92.
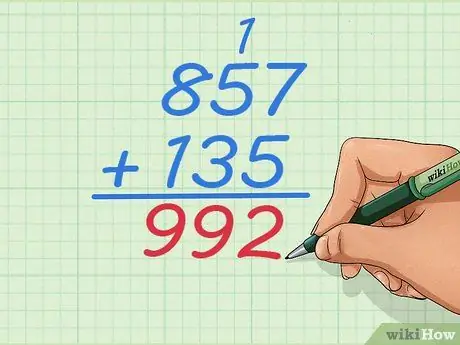
Trin 7. Fuldfør problemet som normalt
Bliv ved med at arbejde med cifrene til venstre, indtil du har tilføjet alle tallene, i dette tilfælde er der kun en kolonne tilbage. Dit endelige svar burde være 992.
- Du kan prøve mere komplicerede spørgsmål, f.eks. 974+568. Husk, at når du får et tocifret tal, skal du kun skrive det sidste ciffer som svaret og placere det andet ciffer over kolonnen til venstre, som du vil tilføje derefter. Hvis svaret i den sidste kolonne (yderst til venstre) indeholder to cifre, skal du skrive det ned som dit svar.
- Se afsnittet Tips for at få svar på spørgsmål 974+568, når du har forsøgt at løse dem.
Metode 4 af 5: Fratrækning af positive store heltal

Trin 1. Skriv subtraktionsproblemet 4.713 - 502 med det første tal over det andet tal
Skriv det, så 3 er direkte over 2, 1 er over 0, 7 er over 5, og 4 er over emnet.
Du kan skrive 0 under 4, hvis dette hjælper dig med at huske, hvilket tal der er over hvilket nummer. Du kan altid tilføje et 0 foran et tal uden at ændre det. Sørg for at tilføje det før nummeret, ikke efter det

Trin 2. Træk hvert tal nedenfor fra tallet direkte over det
Start altid fra højre. Løs 3-2, 1-0, 7-5 og 4-0, skriv svaret på hvert spørgsmål direkte under de to fratrukne tal.
Resultatet er, 4.211.

Trin 3. Skriv nu spørgsmål 924 - 518 på samme måde
Disse tal har samme antal cifre, så du kan nemt skrive dem ned. Dette problem lærer dig noget om at fratrække heltal, hvis du ikke allerede ved det.

Trin 4. Lær, hvordan du løser det første problem, som er yderst til højre
4 - 8. Dette problem er kompliceret, fordi 4 er mindre end 8, men brug ikke negative tal, men følg disse trin:
- I den øverste række krydser du 2 og skriver 1. 2 skal være til venstre for 4.
- Kryds 4 og skriv 14. Gør dette i et smalt mellemrum, så det er klart, at 14 er over 8. Du kan også skrive 1 foran 4 for at lave 14, hvis der er plads nok.
- Det, du lige har gjort, er at låne 1 fra titallspladsen eller den anden kolonne fra højre og konvertere den til 10 på stedet eller yderst til højre. Når tallet 10 er lig med ti gange tallet 1, så er det det samme.

Trin 5. Løs nu problemerne 14 - 8, og skriv svaret under kolonnen til højre
Det skulle have skrevet 6 på den højre svarlinje.

Trin 6. Udfyld den næste kolonne til venstre ved hjælp af det nye nummer, du skrev ned
Subtraktionen skal være 1 - 1, hvilket er lig med 0.
Dit svar burde nu være 06.

Trin 7. Løs problemet ved at fuldføre den sidste subtraktion, kolonnen længst til venstre
9 - 5 = 4, så dit endelige svar er 406.

Trin 8. Nu løser vi problemet med at trække store tal fra små tal
Antag, at du bliver bedt om at fuldføre 415.990 - 968.772. Skriv det andet tal under det første tal, og du vil indse, at tallet nedenfor er større! Du kan straks se fra det første ciffer til venstre: 9 er større end 4, så tal der starter med 9 er større.
Sørg for at skrive kolonnen korrekt ned, før du sammenligner. 912 ingen større end 5000 kan du fortælle, hvis du skriver kolonnen korrekt, fordi der ikke er tal under 5. Du kan tilføje nul hjælp, f.eks. skrive 912 med 0912, så kolonnen er lig med 5000.

Trin 9. Skriv det mindre tal under det større tal, og tilføj et - tegn foran svaret
Når du trækker et tal fra et mindre tal, er resultatet et negativt tal. Det er bedre at skrive dette tegn, før du trækker fra, så du ikke glemmer at skrive det ned.

Trin 10. For at svare skal du trække det lille tal fra det store tal og huske at skrive - -tegnet
Dit svar vil være negativt, hvilket er angivet med et - tegn. Lade være med forsøger at trække et stort tal fra et lille tal, og gør derefter resultatet negativt; dit svar vil være forkert.
Det nye problem, der skal løses, er: 968.772 -415.990 = -? Se afsnittet Tips for svaret efter at have forsøgt at løse dette problem
Metode 5 af 5: Addition og subtraktion af negative heltal
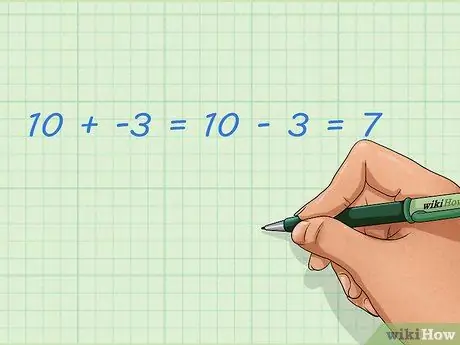
Trin 1. Lær, hvordan du tilføjer negative og positive tal
Tilføjelse af negative heltal er det samme som at trække positive heltal fra. Dette er lettere at gøre med den talelinje, der er beskrevet i et andet afsnit, men du kan også tænke på det med ord. Negative tal er ikke almindelige tal; dette tal er mindre end nul og kan repræsentere det beløb, der er taget. Hvis du tilføjer dette tag til et almindeligt nummer, bliver resultatet mindre.
- Eksempel: 10 + -3 = 10 - 3 = 7
- Eksempel: -12 + 18 = 18 + -12 = 18 -12 = 6. Husk, at du altid kan ændre rækkefølgen af tal derudover, men ikke i subtraktion.
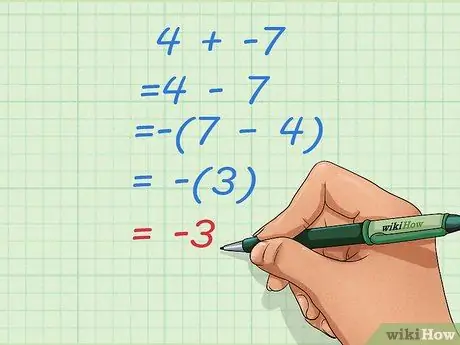
Trin 2. Lær, hvad du skal gøre, hvis du forvandler det til et subtraktionsproblem med et mindre startnummer
Nogle gange kan ændring af tilføjelse til subtraktionsproblemer som ovenstående føre til ulige svar som 4 - 7. Når dette sker, skal du vende rækkefølgen på tallene og gøre dit resultat negativt.
- Lad os sige, at dit første problem er 4 + -7.
- Gør det til et subtraktionsproblem: 4-7
- Vend rækkefølgen, og gør resultatet negativt: -(7 -4) = -(3) = -3.
- Hvis du ikke er bekendt med at bruge parenteser i ligninger, så tænk over dette: 4 - 7 bliver til 7 - 4 med tilføjelse af et negativt tegn. 7 -4 = 3, men vi skal ændre det til -3, så svaret på spørgsmål 4 -7 er korrekt.
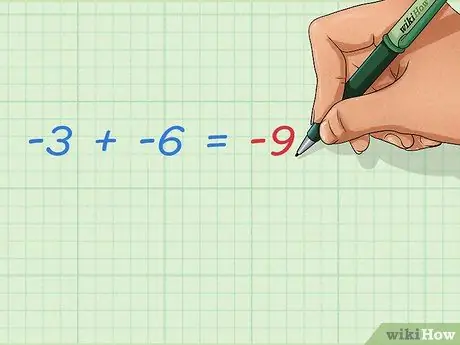
Trin 3. Lær, hvordan du tilføjer to negative heltal
To tilføjede negative tal gør altid det negative resultat større. Da der ikke tilføjes positive tal, vil resultatet være længere væk fra 0. Svaret er let:
- -3 + -6 = -9
- -15 + -5 = -20
- Kan du se mønsteret? Alt du skal gøre er at lægge tallene sammen som om de var positive tal og tilføje et negativt tegn. -4 + -3 = -(4 + 3) = -7
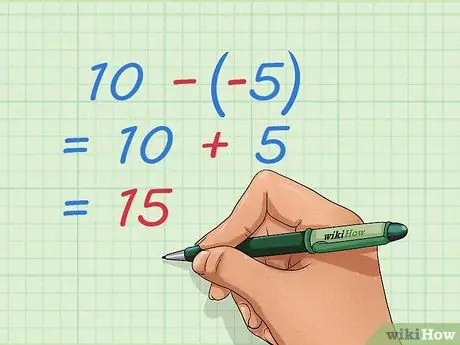
Trin 4. Lær at fratrække negative heltal
Ligesom tilføjelsesproblemet kan du omskrive problemet, så du kun har positive tal. Hvis du trækker negative tal fra, fjerner du nogle af de ting, der allerede er taget, hvilket er det samme som at tilføje positive tal.
- Tænk på negative tal som stjålne penge. Hvis du trækker eller tager stjålne penge fra dig, så du kan returnere dem, er det som at give penge til nogen, ikke?
- Eksempel: 10 --5 = 10 + 5 = 15
- Eksempel: -1 --2 = -1 + 2. Du har allerede lært, hvordan du løser dette problem i det første trin, kan du huske? Læs igen, hvordan du tilføjer negative og positive tal, hvis du har glemt det.
- Her er den komplette løsning af det sidste eksempel: -1 --2 = -1 + 2 = 2 + -1 = 2 -1 = 1.
Tips
- Du har muligvis skrevet lange tal som 2.521.301 ved hjælp af kommaer (,) i stedet for (.) Afhængigt af hvor du bor. Brug det, din lærer beder dig om, så du ikke bliver forvirret med andre skrivesystemer.
- Tegn dine talelinjer på forskellige skalaer for at repræsentere forskellige tal. Der er ingen regel om, at hver afstand på en talelinje er lig med 1. Forestil dig en talelinje, der er 10 i stedet for 1. Bortset fra at hvert punkt er 10 nu, er addition og subtraktion den samme. Prøv det, hvis du ikke tror det.
- Hvis du prøver de særlige udfordringsspørgsmål i afsnittet Lange numre, er her svaret: 974 + 568 = 1.542. Svaret fra 415.990 - 968.772 er - 552.782.







