I maskinteknik er gearforhold en direkte måling af rotationshastigheden for to eller flere gear, der er konkurrencedygtige indkoblet. Som hovedregel ved håndtering af to gear, hvis drivgearet (det gear, der modtager rotationskraften direkte fra motoren, motoren osv.) Er større end det drevne gear, vil det drevne gear rotere hurtigere og omvendt. Vi kan skrive dette grundlæggende koncept i en formel Udvekslingsforhold = T2/T1, T1 er antallet af tænder i det første gear og T2 er antallet af tænder i det andet gear.
Trin
Metode 1 af 2: Beregning af gearforhold i gearkredsløb
To gear
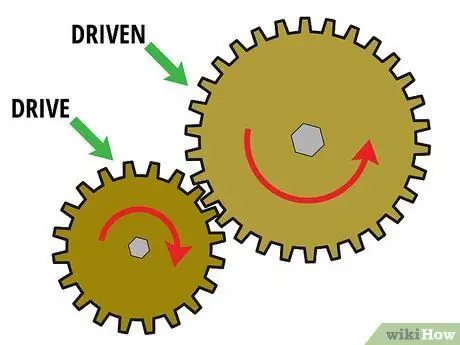
Trin 1. Start med et sæt med to gear
For at bestemme gearforholdet skal du have mindst to gear sammenlåst. Disse to sammenlåsende gear kaldes "gearsæt". Generelt er det første gear et "drivgear" monteret på motorakslen, og det andet gear er et "drevet gear" monteret på lastakslen. Et antal tandhjul kan også være til stede imellem for at overføre kraft fra drivhjulet til det drevne gear. Disse gear kaldes "no-load gear".
Lad os nu se på et gearsæt, der kun har to gear i det. For at beregne gearforholdet skal disse to gear interagere med hinanden. Med andre ord skal tænderne maskes, og den ene skal rotere den anden. Antag f.eks., At du har et lille drivgear (gear 1), der roterer et større drevet gear (gear 2)
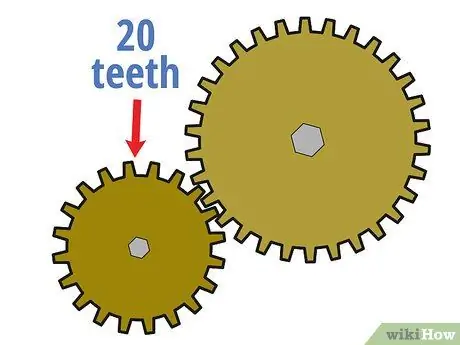
Trin 2. Tæl antallet af tænder på drivgearet
En måde at beregne gearforholdet mellem to sammenlåsende gear er at sammenligne antallet af tænder (små tandlignende stød på kanten af hjulet), de har. Start med at tælle, hvor mange tænder der er i gearet. Du kan gøre dette ved at beregne manuelt eller nogle gange ved at se på de oplysninger, der er trykt på drivhjulet.
Antag f.eks., At det mindre drivgear i systemet har 20 tænder.
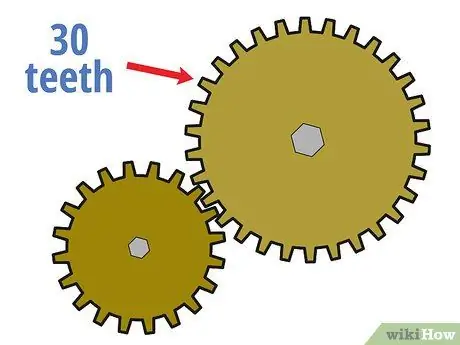
Trin 3. Tæl antallet af tænder på det drevne gear
Tæl derefter, hvor mange tænder der er i det drevne gear, som du gjorde før for drivgearet.
Antag for eksempel, at det drevne gear har 30 tænder.
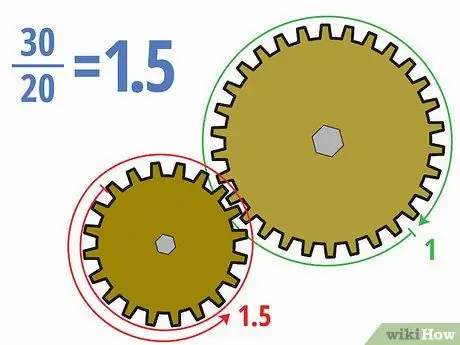
Trin 4. Opdel antallet af tænder med hinanden
Nu hvor du ved, hvor mange tænder der er i hvert gear, kan du forholdsvis let beregne gearforhold. Del tænderne på det drevne gear med tænderne på drivhjulet. Du kan skrive svaret i decimal-, brøk- eller forholdsform (f.eks. X: y) afhængigt af din opgave.
- I eksemplet ovenfor giver dividere 30 tænder i det drevne gear med 20 tænder i drivhjulet 30/20 = 1, 5. Vi kan også skrive det ind 3/2 eller 1, 5: 1.
- Betydningen af dette gearforhold er, at det mindre drivhjul skal rotere halvanden gang for at det større drevne gear skal lave en komplet omdrejning. Fordi det drevne gear er større, vil det drevne gear rotere langsommere.
Mere end to gear
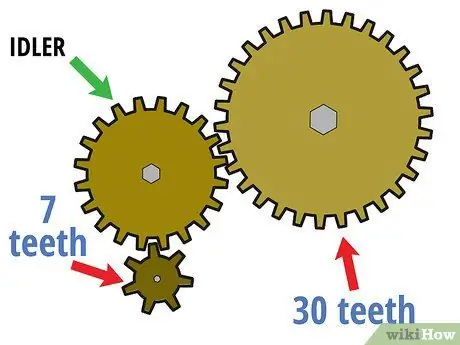
Trin 1. Start med et gearsæt, der har mere end to gear
Som navnet antyder, kan et "gearsæt" sammensættes af en lang række tandhjul, ikke kun et drivgear og et drevet gear. I dette tilfælde forbliver det første gear drivgearet, det sidste gear forbliver det drevne gear, og det midterste gear bliver "ubelastet gear". Disse ubelastede gear bruges ofte til at ændre rotationsretningen eller til at forbinde to gear, når direkte gearjustering ville gøre dem tunge eller utilgængelige.
Antag for eksempel, at det to-gears kredsløb, der er beskrevet ovenfor, nu drives af et gear, der har syv små tænder. I dette tilfælde blev det gear, der havde 30 faste tænder, det drevne gear, og det gear, der havde 20 tænder (som tidligere var drevet) er nu det ubelastede gear
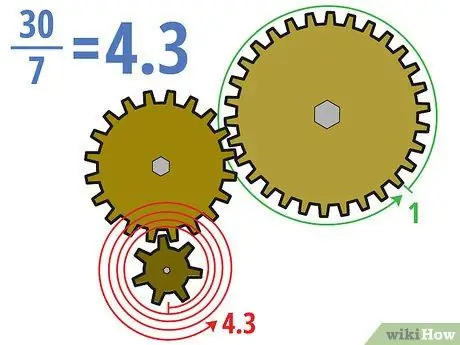
Trin 2. Opdel antallet af tænder på drivgearet og det drevne gear
Den vigtige ting at huske på, når du beskæftiger dig med gearsæt, der har mere end to gear, er, at kun drivgearet og det drevne gear (normalt det første og sidste gear) er vigtige. Med andre ord påvirker tomgangsgear slet ikke gearforholdet for hele sættet. Når du har identificeret drivgear og drevet gear, kan du beregne gearforholdene på samme måde som før.
I eksemplet ovenfor beregner vi gearforholdet ved at dividere de tredive tænder i det drevne gear med de syv tænder i det nye drivhjul. 30/7 = ca. 4, 3 (eller 4, 3: 1). Det betyder, at drivhjulet skal rotere cirka 4,3 gange, for at det meget større drev kan dreje en gang.
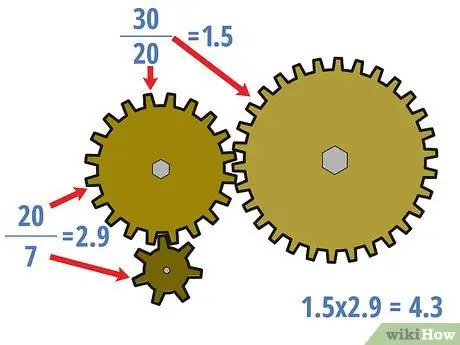
Trin 3. Beregn om nødvendigt gearforholdet for midtergearet
Du kan beregne gearforhold, der også involverer ubelastede gear, og du vil måske gøre det i visse situationer. I dette tilfælde skal du starte ved drivgearet og arbejde dig op til lastgearet. Behandl det forrige gear som et drivhjul helt til det næste gear. Opdel antallet af tænder på hvert "drevet" gear med antallet af tænder på "drev" -gearet for hvert sæt sammenlåsende gear for at beregne det midterste gearforhold.
- I eksemplet ovenfor er centergearforholdet 20/7 = 2, 9 og 30/20 = 1, 5. Det skal bemærkes, at disse forhold ikke er de samme som gearforholdet for hele sættet, hvilket er 4,3.
- Imidlertid, skal det også bemærkes, at (20/7) × (30/20) = 4, 3. Generelt bør forholdet mellem gearets midtergear multipliceres til at svare til forholdet mellem alle gear.
Metode 2 af 2: Udførelse af forhold/hastighedsberegninger
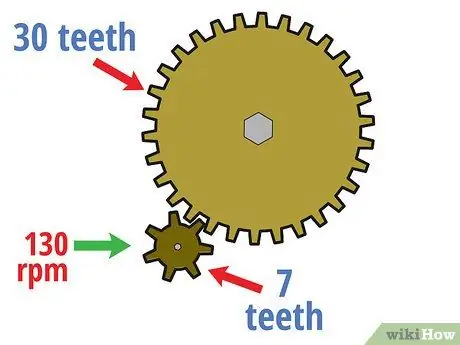
Trin 1. Beregn drevets omdrejningshastighed
Ved hjælp af begrebet gearforhold er det let at bestemme, hvor hurtigt det drevne gear roterer baseret på "input" -hastigheden for drivgearet. For det første skal du beregne omdrejningshastigheden for drivgearet. I mange gearberegninger resulterer dette i omdrejninger pr. Minut (rpm), selvom andre hastighedsenheder også kan bruges.
Antag f.eks. I eksemplet med gearkredsløbet ovenfor med et drivhjul med syv tænder og et drevet gear med 30 tænder, at drivhjulet roterer med en hastighed på 130 omdr./min. Med disse oplysninger vil vi beregne hastigheden på det drevne gear i de følgende trin
Trin 2. Sæt disse oplysninger i formlen S1 × T1 = S2 × T2
I denne formel refererer S1 til drivhjulets rotationshastighed, T1 henviser til tandhjulets tænder, og S2 og T2 henviser til hastigheden og tænderne på det drevne gear. Udfyld disse variabler, indtil du kun har en variabel tilbage.
- Ofte i spørgsmål som dette finder du størrelsen på S2, selvom det er muligt at finde andre variabler. I eksemplet ovenfor får vi:
- 130 rpm × 7 = S2 × 30
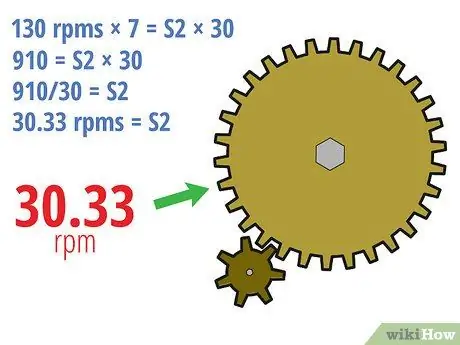
Trin 3. Afslut
Beregning af de resterende variabler er blot et grundlæggende matematisk problem. Forenkle de resterende ligninger og isolere variablen på den ene side af ligningstegnet, og du får svaret. Glem ikke at skrive det i de korrekte enheder. Du kan miste værdi fra lektier på grund af dette.
- I eksemplet ovenfor kan vi løse dette ved at:
- 130 rpm × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30, 33 omdr./min = S2
- Med andre ord, hvis drivhjulet roterer med en hastighed på 130 omdr./min., Vil det drevne gear rotere med en hastighed på 30,33 omdr./min. Da det drevne gear er meget større, vil det drevne gear rotere meget langsommere.
Tips
- For at se, hvordan gearforholdsprincippet gælder, kan du prøve at køre på din cykel. Bemærk, at den letteste måde at klatre på er, når du har et lille gear foran og et stort gear bagpå. Det er lettere at dreje det mindre gear med pedalernes kraft, men det tager mange omdrejninger for baghjulet at dreje i forhold til det gearopsætning, du ville bruge til flade overflader. Dette får dig til at bevæge dig langsommere.
- Et nedgraderet system (når belastningsomdrejningstallet er mindre end motorens omdrejningstal) kræver en motor, der leverer optimal effekt ved højere rotationshastigheder.
- Den krævede effekt for at drive lasten hæves eller sænkes fra motoren gennem gearforholdene. Denne motor skal ændres i størrelse for at levere den effekt, belastningen kræver, efter at gearforholdet er beregnet. Et hævet system (når belastningen RPM er større end motorens omdrejningstal) vil kræve en motor, der leverer optimal effekt ved lavere rotationshastigheder.







