Forskydning i fysik betegner en ændring i objektets position. Når du beregner forskydning, beregner du, hvor langt væk et objekt er baseret på dets indledende og sidste placering. Den formel, du bruger til at beregne forskydning, afhænger af variablen, der er givet til problemet. Følg disse trin for at beregne forskydning.
Trin
Del 1 af 5: Beregning af den resulterende forskydning

Trin 1. Brug den resulterende forskydningsformel, hvis afstandsenheden bruges til at angive dine start- og slutplaceringer
Selvom afstanden er forskellig fra forskydning, ser det resulterende forskydningsproblem efter, hvor mange kilometer eller meter objektet har tilbagelagt. Du vil bruge denne måleenhed til at beregne forskydning, og hvor langt væk et objekts placering afviger fra dets startpunkt.
- Den resulterende forskydningsformel er skrevet som: S = x²+y². S er forskydning. X er objektets første bevægelsesretning og Y er objektets anden bevægelsesretning. Hvis dit objekt kun bevæger sig i en retning, så er Y = 0.
- Et objekt kan kun bevæge sig i maksimalt to retninger, fordi bevægelse langs en nord/syd eller øst/vest akse betragtes som neutral bevægelse.

Trin 2. Forbind prikkerne i bevægelsesrækkefølge, og mærk dem fra A-Z
Brug en lineal til at tegne en lige linje fra punkt til punkt.
- Husk også at forbinde dit udgangspunkt med dit slutpunkt ved hjælp af en lige linje. Dette er forskydningen, vi vil beregne.
- For eksempel, hvis et objekt bevæger sig øst 300 m og nord 400 m, danner det en retvinklet trekant. AB vil være det første ben i trekanten, og BC vil være det andet ben. AC vil være trekantsens hypotenuse, og dens størrelse er objektets forskydning. I dette eksempel er de to retninger øst og nord.

Trin 3. Indtast værdier for x² og y²
Nu hvor du kender objektets to bevægelsesretninger, skal du indtaste værdierne i de relevante variabler.
For eksempel x = 300 og y = 400. Din formel skal se sådan ud: S = 300² + 400²
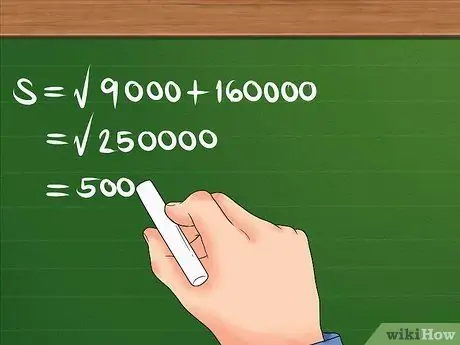
Trin 4. Beregn formlen ved hjælp af rækkefølgen af operationer
Kvadrat 300 og 400 først, tilføj dem derefter, og find kvadratroden af summen.
For eksempel: S = 90000 + 160000. S = 250000. S = 500. Nu ved du, at forskydningen er 500 m
Del 2 af 5: Når hastighed og tid er kendt

Trin 1. Brug denne formel, når problemet fortæller dig et objekts hastighed og den tid, det tager
Nogle matematiske problemer fortæller dig ikke, hvor langt eller hvor hurtigt et objekt bevæger sig. Du kan beregne forskydning ved hjælp af denne størrelse af tid og hastighed.
-
I dette tilfælde bliver formlen: S = 1/2 (u + v) t.
U = objektets starthastighed, eller hvor hurtigt objektet begynder at bevæge sig i en bestemt retning. V = objektets sluthastighed, eller hvor hurtigt objektet bevæger sig mod dets endelige placering. T = den tid, det tager objektet at nå sin endelige placering.
- Eksempel: En bil kører ad vejen i 45 sekunder (krævet tid). Bilen drejer mod vest med 20 m/s (starthastighed), og ved enden af vejen er dens hastighed 23 m/s (sluthastighed). Beregn forskydningen baseret på disse faktorer.

Trin 2. Indtast den nødvendige hastighed og tid i de relevante variabler
Nu hvor du ved, hvor langt bilen kører, hvor hurtigt bilen kører ved start og slutning, kan du finde afstanden fra startstedet til det endelige sted.
Din formel skal se sådan ud: S = 1/2 (20 + 23) 45

Trin 3. Beregn formlen, når du har sat værdierne på det korrekte sted
Husk at følge rækkefølgen af operationer, ellers vil forskydningerne resultere i meget forskellige værdier.
- For denne formel er det ligegyldigt, hvis du ved et uheld bytter start- og sluthastighed. Da du først vil tilføje disse tal sammen, er det ligegyldigt, hvor de er i parentes. For andre formler vil udskiftning af initial- og sluthastighederne imidlertid resultere i forskellige forskydningsværdier.
- Din formel skal se sådan ud: S = 1/2 (43) 45. Divider først 43 med 2, hvilket resulterer i 21, 5. Gang derefter 21, 5 med 45, så resultatet er 967,5 meter. 967, 5 er størrelsen af din forskydning, eller hvor langt din bil har bevæget sig fra startpunktet.
Del 3 af 5: Når initialhastigheden, accelerationen og tiden kendes
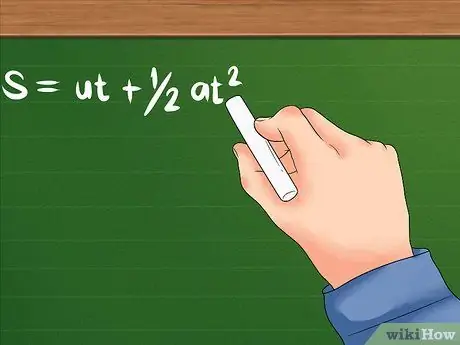
Trin 1. Brug den modificerede formel, når accelerationen er kendt ud over den indledende hastighed og tid
Nogle spørgsmål vil kun fortælle dig, hvor hurtigt objektet bevæger sig i begyndelsen, hvor hurtigt objektet begynder at accelerere, og hvor langt objektet bevæger sig. Du skal bruge følgende formel.
- Formlen for dette problem er: S = ut + 1/2at². U angiver stadig starthastigheden; a er objektets acceleration, eller hvor hurtigt dets hastighed begynder at ændre sig. T kan betyde den tid det tager eller en vis tid det tager et objekt at accelerere. Begge vil bruge tidsenheder som sekunder, timer og andre.
- Antag, at en bil, der kører med 25 m/s (initialhastighed) begynder at accelerere med 3 m/s2 (acceleration) i 4 sekunder (tid). Hvad er forskydningen af bilen efter 4 sekunder?

Trin 2. Indtast værdierne i formlen
I modsætning til den tidligere formel er kun starthastigheden repræsenteret her, så sørg for at indtaste de korrekte data.
Baseret på eksempeldataene ovenfor vil din formel se sådan ud: S = 25 (4) + 1/2 (3) 4². Det hjælper med at tilføje parenteser omkring din accelerationsstørrelse og tid for at hjælpe dig med at adskille tallene
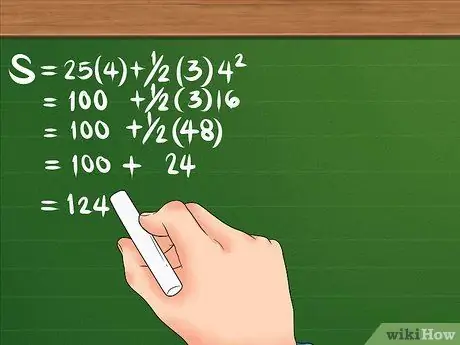
Trin 3. Beregn forskydningen ved at gøre det i den korrekte rækkefølge
En hurtig måde at hjælpe dig med at huske rækkefølgen af operationer er æselbroen Kur ir Kua ci Kadang Ba wa Juragan Turtles. Dette repræsenterer den korrekte rækkefølge: parenteser, firkanter, multiplikation, division, addition og subtraktion.
Lad os se på formlen igen: S = 25 (4) + 1/2 (3) 4². Først, firkant 4, er resultatet 16. Derefter ganges 16 med 3, hvilket gør 48; gang derefter også 25 med 4, for at lave 100. Divider 48 med 2, for at lave 24. Din ligning skal se sådan ud: S = 100 + 24. Når du lægger de to sammen, er forskydningen 124 meter
Del 4 af 5: Beregning af vinkelforskydning

Trin 1. Find vinkelforskydningen, når objektet bevæger sig i en cirkulær bane
Selvom du stadig vil beregne forskydning ved hjælp af en lige linje, skal du finde forskellen mellem objektets start- og slutplaceringer, når det bevæger sig i en cirkulær sti.
- Forestil dig en pige, der sidder på et lysthus. Når han snurrer med karrusellen, vil han bevæge sig i en cirkulær sti. Vinkelforskydning forsøger at finde den korteste afstand mellem de indledende og sidste steder, når objektet ikke bevæger sig i en lige linje.
- Formlen for vinkelforskydning er: = S/r, hvor S er den lineære forskydning, r er radius og er vinkelforskydningen. Lineær forskydning er, hvor langt et objekt bevæger sig langs en bue. Radius er objektets afstand til midten af cirklen. Vinkelforskydning er den værdi, vi ønsker at finde.

Trin 2. Sæt den lineære forskydning og radius i ligningen
Husk, at radius er afstanden fra midten af cirklen; nogle problemer vil fortælle dig en cirkels diameter, som skal divideres med 2 for at finde radius.
- Her er et eksempel på et problem: En pige kører i lystgade. Sædet er 1 meter fra midten af cirklen (radius). Hvis pigen bevæger sig i en lysbue 1,5 meter (lineær forskydning), hvad er hendes vinkelforskydning?
- Din ligning vil se sådan ud: = 1.5/1.
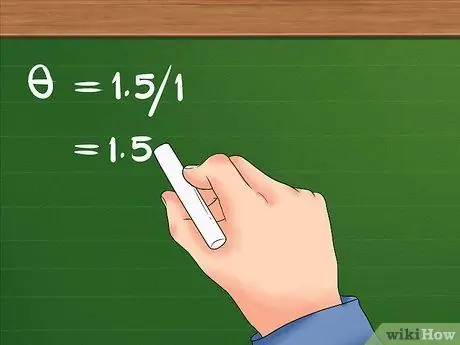
Trin 3. Divider den lineære forskydning med radius
Denne opdeling vil resultere i objektets vinkelforskydning.
- Efter at have delt 1,5 med 1 er resultatet 1,5. Pigens vinkelforskydning er 1,5 radianer.
- Da vinkelforskydning måler, hvor meget et objekt roterer fra dets udgangsposition, skal det måles som en vinkel, ikke en afstand. Radian er den enhed, der bruges til at måle vinkler.
Del 5 af 5: Forståelse om migration
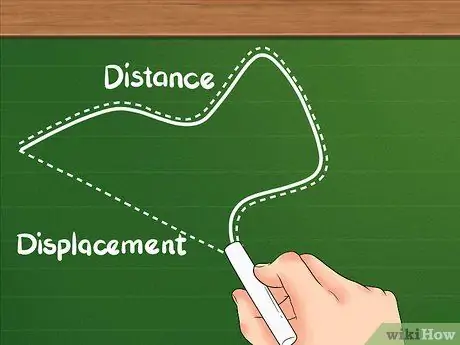
Trin 1. Ved, at afstand har en anden definition end forskydning
Afstand viser, hvor langt den samlede afstand tilbagelagt af objektet.
- Afstand er ofte kendt som en skalær mængde. Afstand viser afstanden tilbagelagt af et objekt uanset objektets retning.
- Hvis du f.eks. Går 2 trin mod øst, 2 trin mod syd, 2 trin mod vest og derefter 2 trin mod nord, vender du tilbage til din startposition. Selvom du har gennemgået totalen afstand 10 skridt væk, du bare bevæge sig 0 skridt væk, fordi din endelige placering er den samme som din startplacering (din sti ligner en boks).

Trin 2. Forstå, at forskydning er forskellen mellem to placeringer
Forskydning er ikke den samlede bevægelsessum som afstand; skift fokuserer på området mellem dine start- og slutsteder.
- Forskydning kaldes en vektormængde og viser ændringen i objektets position ved at overveje objektets bevægelsesretning.
- For eksempel går du øst for 5 trin. Hvis du går 5 trin tilbage vest, bevæger du dig i den modsatte retning fra din oprindelige placering. Selvom du har dækket 10 trin, har din position ikke ændret sig; din forskydning er 0 trin.

Trin 3. Husk ordene frem og tilbage, når du prøver at forestille dig forskydning
Bevægelse i den modsatte retning eliminerer forskydning af et objekt.
Forestil dig en fodboldtræner frem og tilbage på sidelinjen. Da han råbte til spillerne, skiftede han flere gange fra venstre mod højre. Hvis du ser ham, mens han bevæger sig fra venstre mod højre, observerer du den samlede afstand, han har tilbagelagt. Antag dog, at træneren stopper for at tale med quarterbacken på sidelinjen. Hvis han er på et andet tidspunkt end sin oprindelige placering, før han flytter, så observerer du trænerens bevægelse

Trin 4. Ved, at forskydning måles ved hjælp af en lige sti, ikke en cirkelbane
For at finde forskydning skal du finde den korteste og mest effektive måde at beregne forskellen mellem to punkter.
- En cirkulær sti tager dig fra din startplacering til din endelige placering, men det er ikke den korteste vej. For at hjælpe dig med at visualisere det, skal du forestille dig, at du går i en lige linje, og du støder på en søjle. Du kan ikke bryde igennem denne søjle, så du går rundt om den. Selvom din endelige position er den samme, som hvis du brød igennem søjlen, skal du bruge ekstra trin for at nå det mål.
- Selvom forskydning repræsenterer en lige sti, ved du, at du kan måle forskydningen af et objekt, der er i øjeblikket bevæge sig i en cirkulær sti. Denne forskydning kaldes vinkelforskydning og kan beregnes ved at finde den korteste vej fra den oprindelige placering til den endelige placering.

Trin 5. Ved, at forskydning kan være negativ, i modsætning til afstand
Hvis din endelige placering nås ved at bevæge dig i den modsatte retning af din oprindelige retning, er din forskydning negativ.
- For eksempel går vi 5 trin øst og derefter 3 trin mod vest. Selvom du ved beregning bevæger dig 2 trin fra din startplacering, er din forskydning -2, fordi du bevæger dig i den modsatte retning. Din afstand vil altid være positiv, fordi du ikke kan tælle baglæns i trin, kilometer osv.
- Negativ forskydning betyder ikke, at forskydningen falder. Negativ betyder bare, at retningen er modsat.

Trin 6. Indse, at nogle gange kan afstand og forskydning være det samme
Hvis du går lige i 25 trin og stopper, vil afstanden, du rejser, være lig forskydningen fra din oprindelige placering.
- Dette gælder kun, når du flytter fra et sted fra din startposition i en lige linje. For eksempel bor du i San Francisco, Californien, og får et nyt job i Las Vegas, Nevada. Du skal flytte til Las Vegas for at være tæt på dit job. Hvis du stiger på et fly, der flyver lige fra San Francisco til Las Vegas, vil du rejse den samme afstand og forskydning x.
- Men hvis du kører fra San Francisco til Las Vegas, rejser du en afstand x, men rejser en afstand y. Da kørsel i en bil normalt har varierende retninger (øst for denne vej, vest for den vej), vil du rejse længere strækninger end den korteste afstand mellem de to byer.







