Sådan lærer du matematik (med billeder)

2024 Forfatter: Jason Gerald | [email protected]. Sidst ændret: 2024-02-01 14:12

Alle kan lære matematik, uanset om de allerede er på et højere trin i skolen, eller som bare vil finpudse det grundlæggende igen. Efter at have diskuteret, hvordan du bliver en god elev i matematik, vil denne artikel lære dig de grundlæggende matematiske fremskridt og give dig de grundlæggende elementer, du skal lære i hver øvelse. Derefter vil denne artikel diskutere det grundlæggende i at lære regning, som vil hjælpe både folkeskolebørn og alle, der ønsker at lære det grundlæggende inden for dette videnskabelige felt.

Trin

Del 1 af 6: Nøgler til at blive en god matematikstuderende

Trin 1. Vises i klassen

Når du går glip af klassen, bør du lære begreber fra klassekammerater eller fra din lærebog. Du får aldrig en tekstoversigt fra en ven så meget, som du får fra din lærer.

Kom til time til tiden. Kom i stedet lidt tidligt og åbn din notesbog det rigtige sted, åbn din lærebog og tag din lommeregner ud, så du er klar til at starte, når din lærer er klar til at undervise.
Kun truant, hvis du er syg. Hvis du virkelig savner klassen, skal du bede dine klassekammerater finde ud af, hvad læreren talte om, og hvilke lektier der blev givet.

Trin 2. Arbejd med din lærer

Hvis din lærer arbejder på et problem foran klassen, skal du arbejde med læreren ved at arbejde med problemet i din notesbog.

Sørg for, at dine noter er klare og lette at læse. Skriv ikke bare spørgsmål. Skriv også ned alt, hvad læreren siger, der kan forbedre din forståelse af de begreber, der forklares.
Udfyld eksemplerne på spørgsmål fra din lærer. Mens læreren går rundt i klassen, mens du arbejder, skal du besvare de spørgsmål, der stilles.
Deltag, når læreren løser et problem. Vent ikke på, at læreren ringer til dig. Tilbyd at svare, når du kender svaret, og løft din hånd for at stille et spørgsmål, hvis du er i tvivl om det materiale, der undervises i.

Trin 3. Gør dit hjemmearbejde samme dag, som dit hjemmearbejde gives

Hvis du laver dit hjemmearbejde samme dag, er konceptet stadig frisk i tankerne. Nogle gange er det ikke muligt at afslutte dit hjemmearbejde samme dag. Sørg for, at dit hjemmearbejde er færdigt, før du går i klasse.

Trin 4. Arbejd uden for klassen, hvis du har brug for hjælp

Besøg din lærer i pauser eller i kontortid.

Hvis du har et matematikcenter på din skole, skal du finde ud af åbningstiderne og bede om hjælp.
Deltag i en studiegruppe. En god studiegruppe består generelt af 4 eller 5 personer med forskellige evner. Hvis du er en "C" -studerende i matematik, skal du deltage i en gruppe på 2 eller 3 elever med "A" eller "B" karakterer, så du kan forbedre dine færdigheder. Undgå at deltage i en gruppe elever, hvis karakterer er lavere end dine.

Del 2 af 6: Læring af matematik i skolen

Trin 1. Start med regning

På de fleste skoler lærer eleverne regning i folkeskolen. Aritmetik dækker det grundlæggende ved addition, subtraktion, multiplikation og division.

Lav øvelsesspørgsmål. At lave regneopgaver igen og igen er den bedste måde at huske det grundlæggende korrekt på. Kig efter software, der kan give dig en lang række forskellige matematiske problemer at arbejde med. Se også efter problemer med tidsrammer for at forbedre din hastighed.
Du kan også finde regningsproblemer online, og du kan downloade aritmetiske apps til din mobile enhed.

Trin 2. Fortsæt med præ-algebraen

Denne øvelse giver dig de grundlæggende elementer, du skal bruge til at løse algebra -problemer senere.

Lær om brøker og decimaler. Du lærer at tilføje, trække, multiplicere og dividere brøker og decimaler. Hvad angår brøker, lærer du at fratrække brøker og oversætte kombinerede tal. Hvad angår decimaler, forstår du stedværdier, og du vil kunne bruge decimaler i historieproblemer.
Lær om forhold, proportioner og procenter. Disse begreber hjælper dig med at lære at foretage sammenligninger.
Introducer dig selv for grundlæggende geometri. Du lærer 3D former og koncepter. Du lærer også begreber som areal, omkreds, volumen og overfladeareal samt information om parallelle og vinkelrette linjer og vinkler.
Forstå nogle grundlæggende statistikker. I præ-algebra indeholder din introduktion til statistik generelt grafik som grafer, spredningsdiagrammer, stempeldiagrammer og histogrammer.
Lær det grundlæggende i algebra. Dette inkluderer begreber som at løse simple ligninger, der indeholder variabler, lære om egenskaber som den fordelende egenskab, tegne simple ligninger og løse uligheder.

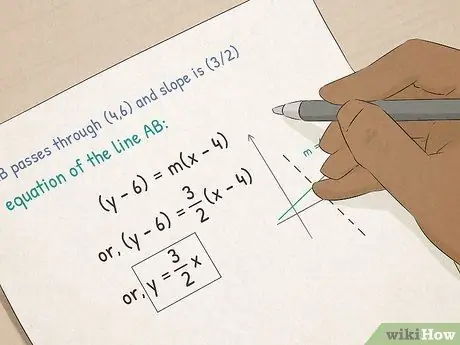
Trin 3. Gå videre til Algebra I

I dit første år med algebra lærer du om de grundlæggende symboler, der er inkluderet i algebra. Du vil også lære at:

Løs ligninger og uligheder, der indeholder variabler. Du lærer, hvordan du løser disse problemer på papir, og hvordan du løser dem med billeder.
Løs historieproblemer. Du vil blive overrasket over, hvor mange hverdagsproblemer du vil møde i fremtiden, der kræver evnen til at løse algebraiske historieproblemer. For eksempel vil du bruge algebra til at finde ud af den rente, du tjener på din bankkonto eller investering. Du kan også bruge algebra til at finde ud af, hvor længe du skal rejse baseret på din bils hastighed.
Arbejde med eksponenter. Når du begynder at løse polynomiske ligninger (udtryk, der indeholder tal og variabler), forstår du, hvordan du bruger eksponenter. Dette vil sandsynligvis omfatte øvelser med videnskabelig notation. Når du mestrer eksponenter, kan du lære at tilføje, trække fra, gange og dividere polynomiske udtryk.
Løs kvadrat- og kvadratrodsproblemer. Når du mestrer dette emne, vil du kunne huske firkanterne med mange tal. Du vil også kunne arbejde med ligninger, der har kvadratrødder.
Forstå funktioner og grafer. I algebra lærer du om grafiske ligninger. Du lærer, hvordan du beregner hældningen af en linje, hvordan du sætter en ligning i form-hældningsform, og hvordan du beregner x-og-y-skiven af en linje ved hjælp af hældnings-skæringsformen.
Find ud af ligningssystemet. Nogle gange får du 2 forskellige ligninger med variablerne x og y, og du skal løse for x eller y for begge ligninger. Heldigvis lærer du en masse tricks til at løse disse ligninger, herunder grafer, substitution og tilføjelse.

Trin 4. Undersøg geometri

I geometri lærer du om egenskaberne ved linjer, segmenter, vinkler og former.

Du vil huske en række sætninger og konsekvenser, der hjælper dig med at forstå geometriske regler.
Du vil lære at beregne arealet af en cirkel, hvordan du bruger Pythagoras sætning og hvordan du finder forholdet mellem vinklerne og siderne af en speciel trekant.
Du vil se mange geometri -spørgsmål i fremtidige standardiserede tests som SAT, ACT og GRE.

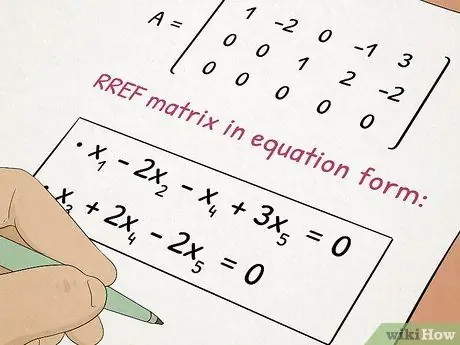
Trin 5. Tag Algebra II -klassen

Algebra II bygger på de begreber, du har lært i Algebra I, mens du tilføjer komplekse emner som kvadratiske ligninger og matricer.

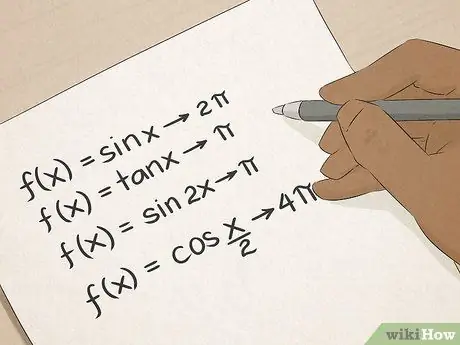
Trin 6. Master trigonometri

Du kender trigonometriske termer: sinus, cosinus, tangens og så videre. Trigonometri lærer dig mange praktiske måder at beregne vinkler og linjelængder på, og disse færdigheder vil være uvurderlige for mennesker, der arbejder inden for byggeri, arkitektur, teknik eller opmåling.

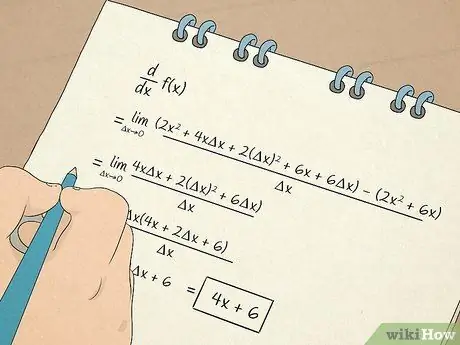
Trin 7. Udfør beregningsberegninger

Regning kan lyde skræmmende, men det er et vidunderligt værktøj til at forstå enten tales adfærd eller verden omkring dig.

Calculus lærer dig funktioner og grænser. Du vil se antallet af funktionaliteter for nyttige funktioner, herunder e^x og logaritmiske funktioner.
Du vil også lære at beregne og arbejde med derivater. Det første derivat giver dig information baseret på tangentlinjens hældning til en ligning. For eksempel fortæller et derivat dig den hastighed, hvormed noget ændrer sig i en ikke-lineær situation. Det andet derivat fortæller dig, om funktionen stiger eller falder over et bestemt interval, så du kan bestemme konkaviteten af en funktion.
Integraler lærer dig, hvordan du beregner arealet under en kurve samt dets volumen.
Regning i gymnasiet ender generelt med sekvenser og sekvenser. Selvom eleverne ikke vil se mange applikationer til kredsløb, er kredsløb vigtige for dem, der studerer differentialligninger.

Del 3 af 6: Math Fundamentals-Master Addition

Trin 1. Start med "+1" fakta

Hvis du tilføjer 1 til et tal, kommer du til det højeste nummer på tallinjen. For eksempel 2 + 1 = 3.

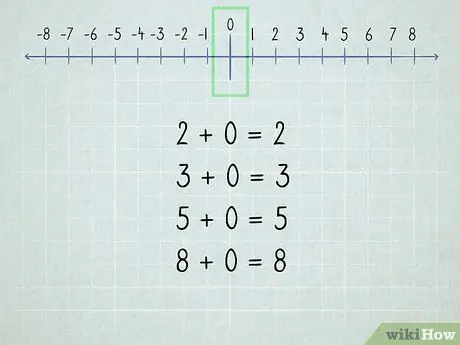
Trin 2. Forstå nul

Alle tal tilføjet til nul er det samme tal, fordi "nul" betyder "ingen".

Trin 3. Lær dobbelttal

Flere tal er et problem, der indebærer at tilføje to lige tal. For eksempel er 3 + 3 = 6 et eksempel på en ligning, der involverer flere tal.

Trin 4. Brug kortlægning til at lære om andre tilføjelsesløsninger

I eksemplet herunder lærer du ved at kortlægge, hvad der sker, når du tilføjer 3 til 5, 2 og 1. Prøv selv problemet "tilføj med 2".

Trin 5. Fortsæt, indtil tallet er mere end 10

Lær at tilføje 3 tal sammen for at få et tal større end 10.

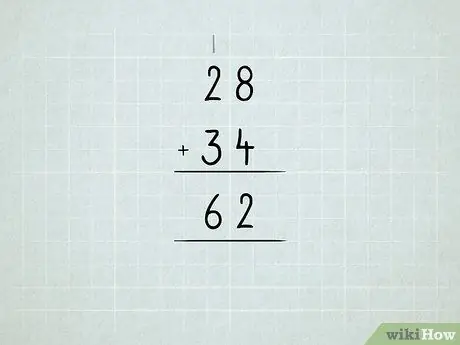
Trin 6. Tilføj de større tal

Lær om omgruppering af enheder i tiere, tiere i hundredvis og så videre.

Tilføj tallene i den højre kolonne først. 8 + 4 = 12, hvilket betyder, at du har 1 nummer 10 og 2 tal 1. Skriv tallet 2 under kolonnen enheder.
Skriv tallet 1 i kolonnen tiere.
Læg kolonnen med tiere sammen i sin helhed.

Del 4 af 6: Matematiske grunde-Reduktionsstrategier

Trin 1. Start med "bagud 1 ciffer

Ved at trække 1 fra et tal tager du 1 tilbage. Eksempelvis 4 - 1 = 3.

Trin 2. Lær at fratrække dobbelttal

For eksempel tilføjer du tallene 5 + 5 for at få 10. Skriv bare ligningen baglæns for at få 10 - 5 = 5.

Hvis 5 + 5 = 10, så er 10 - 5 = 5.
Hvis 2 + 2 = 4, så 4 - 2 = 2.

Trin 3. Husk faktafamilien udenad

Som et eksempel:

3 + 1 = 4
1 + 3 = 4
4 - 1 = 3
4 - 3 = 1

Trin 4. Find de manglende numre

For eksempel _ + 1 = 6 (svaret er 5).

Trin 5. Husk faktum ved subtraktion til 20

Trin 6. Øv dig på at trække 1-cifrede tal fra 2-cifrede tal uden at låne

Træk tallene i ene -kolonnen og reducer tallene i kolonnen tiere.

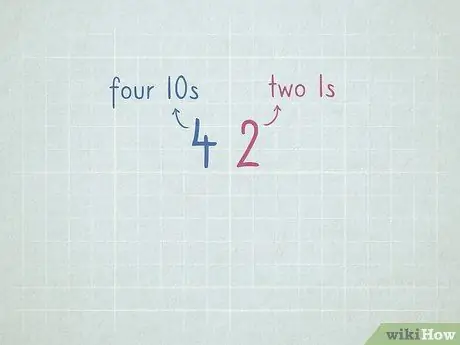
Trin 7. Øv stedværdi for at forberede til at trække fra ved lån

32 = 3 tal 10 og 2 tal 1.
64 = 6 tal 10 og 4 tal 1.
96 = _ nummer 10 og _ nummer 1.

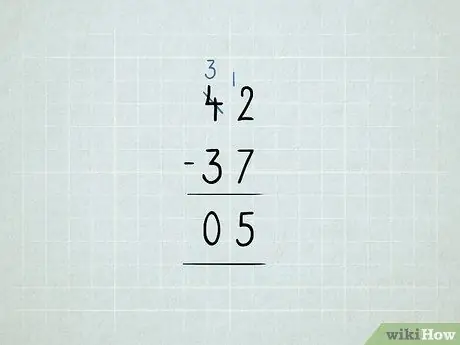
Trin 8. Træk fra ved at låne

Du vil trække fra 42 - 37. Du starter med at prøve at trække fra 2 - 7 i kolonnen enheder. Det viste sig, at det ikke virkede!
Lån tallet 10 fra kolonnen tiere, og placer det i kolonnen dem. Nu har du 3 10'er i stedet for 4 10. Nu har du 12 1'er i stedet for 2 1'er.
Træk først din enheds kolonne: 12 - 7 = 5. Kontroller derefter kolonnen tiere. Da 3 - 3 = 0, behøver du ikke at skrive tallet 0. Dit svar er 5.

Del 5 af 6: Grundlæggende matematik-Master multiplikation

Trin 1. Start med tallet 1 og tallet 0

Alle tal, der ganges med 1, er de samme som selve tallet. Ethvert tal ganget med 0 er lig med nul.

Trin 2. Gem multiplikationstabellen udenad

Trin 3. Træn med enkeltcifrede multiplikationsproblemer

Trin 4. Multiplicer det 2-cifrede nummer med det 1-cifrede nummer

Gang det nederste højre nummer med det øverste højre nummer.
Gang det nederste højre nummer med det øverste venstre nummer.

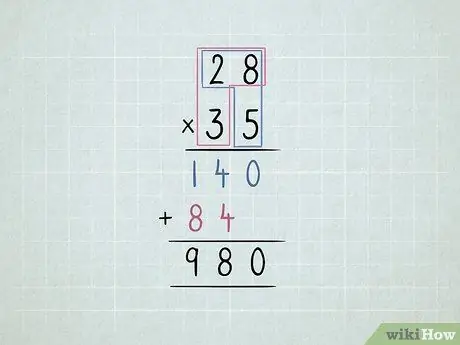
Trin 5. Multiplicer 2 2-cifrede tal

Gang det nederste højre nummer med det øverste højre nummer og derefter med det øverste venstre nummer.
Flyt den anden række et ciffer til venstre.
Gang det nederste venstre nummer med det øverste højre nummer og derefter det øverste venstre nummer.
Tilføj alle kolonner.

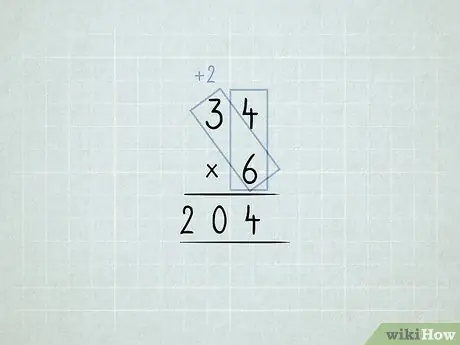
Trin 6. Multiplicer og omgrupper kolonnerne

Du vil multiplicere 34 x 6. Du starter med at gange enhedens kolonne (4 x 6), men du kan ikke have 24 1'er i kolonnen med dem.
Gem 4 1'er i enhedskolonnen. Flyt 2 10'er til kolonnen tiere.
Multiplicer 6 x 3, hvilket svarer til 18. Tilføj de 2, du flyttede, hvilket er lig med 20.

Del 6 af 6: Matematiske grunde-Afslør divisionsproblemer

Trin 1. Tænk på division i modsætning til multiplikation

#* Hvis 4 x 4 = 16, så 16 /4 = 4.

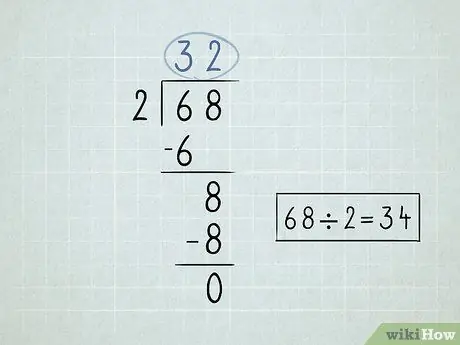
Trin 2. Skriv dit delingsproblem op

Divider nummeret til venstre for divisionssymbolet, eller divisor, med det første tal under divisorsymbolet. Da 6 /2 = 3, ville du skrive tallet 3 over divisionssymbolet.
Multiplicer tallet over divisionssymbolet med divisoren. Bring resultatet ned til bunden af det første tal under divisionssymbolet. Da 3 x 2 = 6, så vil du sænke tallet 6 ned.
Træk de 2 tal, du har skrevet ned. 6 - 6 = 0. Du kan efterlade 0 tomt, fordi du generelt ikke starter tal med 0.
Sænk det andet tal, der er under divisionssymbolet.
Opdel det nummer, du bringer ned med divisoren. I dette tilfælde er 8 /2 = 4. Skriv tallet 4 over divisionssymbolet.
Gang det øverste højre nummer med divisoren og bring tallet ned. 4 x 2 = 8.
Træk disse tal fra. Den sidste subtraktion returnerer nul, hvilket betyder, at du har løst problemet. 68 x 2 = 34.

Trin 3. Beregn også resten

Nogle af delerne er ikke fuldstændigt opdelt i andre tal. Hvis du har gennemført den sidste subtraktion, og du ikke har flere tal at udlede, så er det sidste tal resten.