Sådan beregnes gennemsnitshastighed: 12 trin (med billeder)

2024 Forfatter: Jason Gerald | [email protected]. Sidst ændret: 2024-02-01 14:12

Alt hvad du behøver for at beregne gennemsnitshastigheden er den samlede forskydning. eller ændring af position og samlet tid. Husk, at hastighed også beregner retningen og hastigheden af et objekt, så inkluder en retning i dit svar, f.eks. "Nord", "front" eller "venstre". Hvis dit hastighedsberegningsproblem også involverer konstant acceleration, kan du lære en hurtig måde at finde svaret på endnu lettere.

Trin

Metode 1 af 2: Beregning af forskydningens og tidens gennemsnitlige hastighed

Trin 1. Husk, at hastighed omfatter både et objekts hastighed og retning

Hastighed beskriver den hastighed, hvormed et objekts position ændres. Dette har ikke kun at gøre med, hvor hurtigt objektet bevæger sig, men også med dets retning. "100 meter i sekundet mod syd" er en anden hastighedsværdi end "100 meter i sekundet mod øst".

• Mængder, der har retning, kaldes vektormængder '. Denne mængde kan skelnes fra en retningsløs mængde kaldet en skalær mængde ved at skrive en pil over variablen. For eksempel repræsenterer notationen v hastigheden, mens notationen v ^→ repræsenterer hastighed eller hastighed + retning. V -betegnelsen, der bruges i denne artikel, repræsenterer hastighed.
• I videnskabelige problemer bør du bruge målere eller andre metriske enheder til at udtrykke afstand, mens du til daglig brug kan bruge enhver enhed, du kan lide.

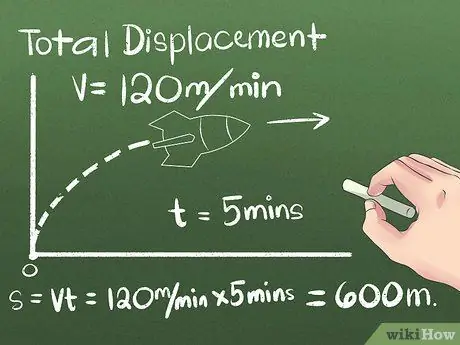
Trin 2. Find den samlede forskydningsværdi

Forskydning er ændringen i et objekts position eller afstanden og retningen mellem dets start- og slutpunkter. Retningen, som objektet bevæger sig, inden det når sin endelige position, kan negligeres, fordi kun afstanden mellem start- og slutpunkter tages i betragtning. For det første eksempel vil vi bruge et objekt, der bevæger sig med en konstant hastighed i en retning:

• Lad os sige, at en raket bevæger sig nordpå i 5 minutter med en konstant hastighed på 120 meter i minuttet. For at beregne den endelige position skal du bruge formlen s = vt, eller bruge praktisk tænkning til at beregne den afstand, raketten har tilbagelagt efter det (5 minutter) (120 meter/minut) = 600 meter nord fra udgangspunktet.
• Ved problemer med konstant acceleration kan du løse dem med s = vt + at²eller brug den korte metode beskrevet i et andet afsnit for at finde svaret.

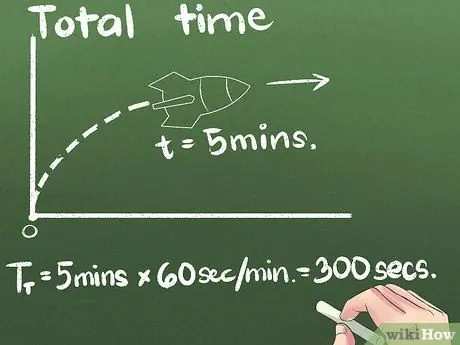
Trin 3. Find den samlede brugte tid

I vores eksempel bevæger raketten sig fremad i 5 minutter. Du kan udtrykke gennemsnitshastigheden i enhver tidsenhed, men den anden er den internationale videnskabelige standardenhed. Vi vil ændre enhederne i sekunder i dette eksempel: (5 minutter) x (60 sekunder/minut) = 300 sekunder.

Selv i videnskabelige problemer, hvis spørgsmålet bruger timen eller en større tidsenhed, vil det være lettere at beregne hastigheden først og derefter konvertere det endelige svar til meter/sekund

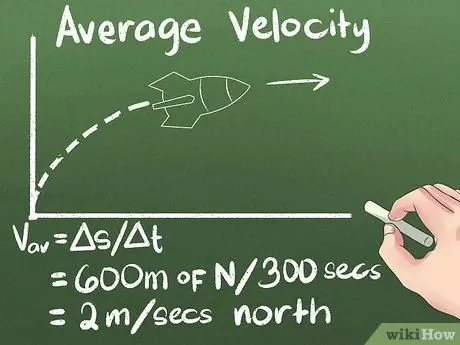
Trin 4. Beregn gennemsnitshastigheden som forskydning over tid

Hvis du ved, hvor langt et objekt bevæger sig, og hvor lang tid det vil tage at komme dertil, ved du, hvor hurtigt det bevæger sig. Så for det eksempel, vi bruger, er raketens gennemsnitshastighed (600 meter nord) / (300 sekunder) = 2 meter/sekund nordpå.

• Husk at inkludere en retning (f.eks. "Front" eller "nord").
• I formlen v_av = s/Δt. Delta -symbolet betyder "ændring", så s/Δt betyder "ændring i position over en periode."
• Gennemsnitshastigheden kan skrives som v_aveller som et v med en vandret linje over det.

Trin 5. Løs mere komplicerede problemer

Hvis et objekt ændrer retning eller hastighed, skal du ikke blive forvirret. Gennemsnitshastighed er stadig "kun" beregnet ud fra total forskydning og samlet tid. Hvad der sker mellem start- og slutpunkterne, kan du ignorere. Følgende er nogle eksempler på et objekt, der rejser med samme forskydning og samlede tid og dermed den samme gennemsnitshastighed:

• Anna går vestpå med 1 meter/s i 2 sekunder, så accelererer den pludselig til 3 meter/sekund og fortsætter med at gå vest i 2 sekunder. Den samlede forskydning er (1 m/s vestpå) (2 sek) + (3 m/s vestpå) (2 sek) = 8 meter vestpå. Den samlede tid er 2 sekunder + 2 sekunder = 4 sekunder. Så gennemsnitshastigheden er 8 meter vest/ 4 sekunder = 2 meter/andet vest.

• Bart går vestpå med 5 meter/sek i 3 sekunder, vender derefter om og går østpå med 7 meter/sek i 1 sekund. Vi kan tænke på den østlige bevægelse som "negativ vestlig bevægelse", så den samlede forskydning er = (5 meter/sek vest) (3 sek) + (-7 m/s vest) (1 sek) = 8 meter. Samlet tid = 4 sekunder. Gennemsnitshastighed = 8 meter vest / 4 sekunder = 2 meter/andet vest.

• Charlotte gik nordpå 1 meter og gik derefter vest 8 meter, derefter syd 1 meter. Den tid det tager at fuldføre hele rejsen er 4 sekunder. Tegn diagrammet på et stykke papir, og du vil se slutpunktet er 8 meter vest for startpunktet, så denne værdi er forskydningen. Den samlede tid det tager er 4 sekunder, så gennemsnitshastigheden er 8 meter vest / 4 sekunder = 2 meter/andet vest.

  Metode 2 af 2: Beregning af gennemsnitshastigheden for fast acceleration

  

  Trin 1. Overvej initialhastigheden og konstant acceleration

  Lad os sige, at vores problem er "En cykel bevæger sig til højre med en hastighed på 5 m/s, med en konstant acceleration på 2 m/s². Hvis denne cykel bevæger sig i 5 sekunder, hvad er dens gennemsnitlige hastighed?"

  Hvis enheden "meter/sekund²"for at forvirre dig, skriv det som" meter/sekund/sekund "eller" meter i sekundet. "En acceleration på 2 meter/sekund/sekund betyder, at hastigheden stiger med 2 meter i sekundet hvert sekund.

  

  Trin 2. Brug acceleration til at finde den endelige hastighed

  Acceleration, betegnet med notationen a, er hastigheden for ændring af hastighed (eller hastighed). Hastigheden stiger med en konstant stigningshastighed. Du kan tegne et bord ved hjælp af acceleration for at finde hastigheden på forskellige tidspunkter under cykelturen. Vi skal oprette denne tabel for at finde slutpunktet for problemet (ved t = 5 sekunder), men vi opretter en længere tabel for at gøre det lettere for dig at forstå dette koncept:

  • Ved startpunktet (tid t = 0 sekunder) bevæger cyklen sig med en hastighed på 5 meter/s.
  • Efter 1 sekund (t = 1) kører cyklen med en hastighed på 5 meter/sekund + ved = 5 meter/sekund + (2 meter/sekund²) (1 sekund) = 7 meter/sekund.
  • Ved t = 2 bevæger cyklen sig til højre med en hastighed på 5+ (2) (2) = 9 meter/sek.
  • Ved t = 3 bevæger cyklen sig til højre med en hastighed på 5+ (2) (3) = 11 meter/sek.
  • Ved t = 4 bevæger cyklen sig til højre med en hastighed på 5+ (2) (4) = 13 meter/sek.
  • Ved t = 5 bevæger cyklen sig til højre med en hastighed på 5+ (2) (5) = 15 meter/sekund.

  

  Trin 3. Brug denne formel til at finde gennemsnitshastigheden

  Hvis og "kun" hvis accelerationen er konstant, vil gennemsnitshastigheden være lig med gennemsnitsværdien af summen af slut- og initialhastighederne. (v_f +v_jeg)/2. For vores eksempelproblem ovenfor er cykelens starthastighed v_jeg 5 meter/sekund. Når vi har beregnet, er sluthastigheden v_f 15 meter/sekund. Ved at tilføje disse to værdier får vi (15 meter/sekund + 5 meter/sekund)/2 = (20 meter/sekund)/2 = 10 meter/sekund højre retning.

  • Husk at inkludere retningen, i dette tilfælde "højre".
  • Dette udtryk kan skrives som v₀ (hastighed på tidspunktet 0 eller starthastighed) og v (sluthastighed).

  

  Trin 4. Forstå gennemsnitshastighedsformlen intuitivt

  For at finde gennemsnitshastigheden kan vi bruge hastigheden til enhver tid og finde gennemsnittet for dem alle. (Dette er definitionen på et gennemsnit.) Da dette kræver beregning eller uendelig tid, skal du forstå denne formel mere intuitivt. I stedet for at tage hver gang, skal du beregne gennemsnitshastigheden for de to tidspunkter og se resultaterne. Et tidspunkt er nær starten af turen, hvor cyklen går langsomt, og et andet punkt er nær slutpunktet, hvor cyklen går hurtigt.

  

  Trin 5. Test intuitiv teori

  Brug tabellen ovenfor til at bestemme hastigheden på forskellige tidspunkter. Nogle par, der opfylder vores kriterier, er (t = 0, t = 5), (t = 1, t = 4) eller (t = 2, t = 3). Du kan også teste denne formel med andre t -værdier end heltal, hvis du vil.

  Uanset hvilket par af punkter du vælger, vil gennemsnitshastigheden på det tidspunkt altid være den samme. For eksempel er ((5+15)/2), ((7+13)/2) eller ((9+11)/2) alle 10 meter/sek til højre

  

  Trin 6. Fuldfør den intuitive forklaring

  Hvis vi bruger denne metode med en liste over hver gang, vi tager den, fortsætter vi med at beregne gennemsnittet af første halvdel af turen og anden halvdel af turen. Den tid det tager at dække hver halvleg er den samme, så ingen hastighed går tabt, når vi er færdige med at tælle.

  • Da begge par vil give det samme resultat, vil gennemsnittet af disse hastigheder også være det samme i værdi. I vores eksempel er hastigheden af det hele "10 meter/sek højre" vil stadig være 10 meter/sek til højre.
  • Vi kan finde denne værdi ved at beregne gennemsnittet af et hvilket som helst par, for eksempel initial- og sluthastighederne. I vores eksempel nås disse hastigheder ved t = 0 og t = 5 og kan beregnes ved hjælp af formlen ovenfor: (5+15)/2 = 10 meter/sek til højre.

  

  Trin 7. Forstå denne formel matematisk

  Hvis du er mere fortrolig med beviser nedskrevet som formler, kan du starte med en formel til at beregne den tilbagelagte afstand forudsat konstant acceleration og udlede formlen derfra:

  • s = v_jegt + kl². (Teknisk s og t, eller ændring i position og ændring i tid, men du ville også blive forstået, hvis du skrev s og t.)
  • Gennemsnitshastighed v_av defineret som s/t, så indtast formlen i formen s/t.
  • v_av = s/t = v_jeg + kl
  • Acceleration x tid er lig med ændringen i totalhastighed eller v_f - v_jeg. Så vi kan erstatte "at" i formlen og få:
  • v_av = v_jeg + (v_f - v_jeg).
  • Forenkle: v_av = v_jeg + v_f - v_jeg = v_jeg + v_f = (v_f +v_jeg)/2.

  Tips

  • Hastighed er forskellig fra hastighed, fordi hastighed er en vektormængde, hvorimod hastighed er en skalær mængde. Vektormængder involverer både retning og størrelse, mens skalære mængder kun involverer størrelse.
  • Hvis objektet bevæger sig i en dimension, f.eks. Venstre-højre, kan du bruge et positivt tal til at repræsentere en retning (f.eks. Højre) og et negativt tal til at repræsentere en anden retning (venstre). Skriv denne notation øverst på din side, så det er klart for folk, der læser dit arbejde.