Den normale kraft er størrelsen af den kraft, der kræves for at negere de andre kræfter i ethvert scenario. Den bedste måde at finde det på afhænger af objektets tilstand og de variabler, du har. Fortsæt med at læse for at lære mere.
Trin
Metode 1 af 5: Normal stil i hvile
Trin 1. Forstå betydningen af normal kraft
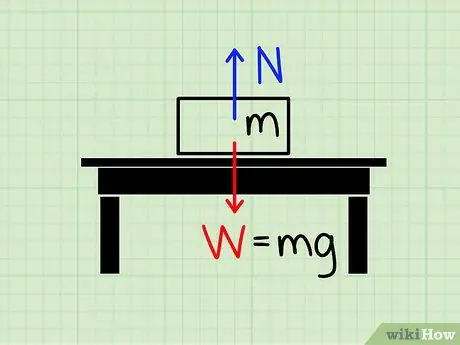
Den normale kraft refererer til størrelsen af den kraft, der bruges til at negere tyngdekraften.
Forestil dig en blok i hvile på et bord. Tyngdekraften trækker blokken mod jorden, men tydeligvis virker der en kraft, der forhindrer blokken i at knuse bordet og falde til jorden. Den kraft, der virker for at stoppe denne blok på trods af tyngdekraften, kaldes normal stil.
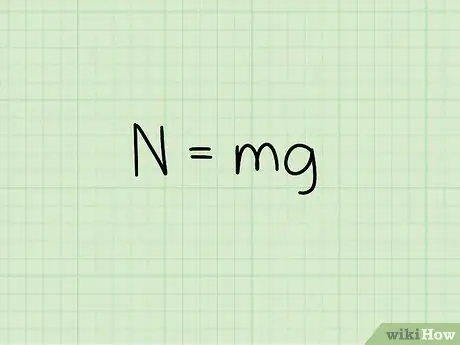
Trin 2. Kend ligningen for den normale kraft på et objekt i hvile
Når du beregner et objekts normale kraft, når det hviler på en flad overflade, skal du bruge formlen: N = m * g
- I denne ligning, N symboliserer normal stil, m repræsenterer objektets masse og g repræsenterer accelerationen på grund af tyngdekraften.
- For et objekt, der hviler på en flad overflade, uden at en ekstern kraft virker, er den normale kraft lig med objektets vægt. For at holde et objekt i ro, skal den normale kraft svare til tyngdekraften, der virker på objektet. Tyngdekraften, der virker på et objekt, er genstandens vægt, eller objektets masse gange accelerationen på grund af tyngdekraften.
- Eksempel: Find den normale kraft af en blok med en masse på 4,2 kg.
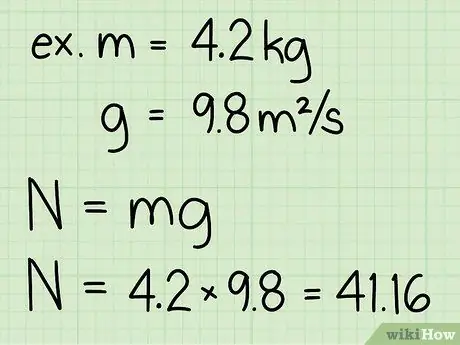
Trin 3. Multiplicer objektets masse og accelerationen på grund af tyngdekraften
Denne multiplikation vil producere objektets vægt, hvilket naturligvis er lig med objektets normale kraft i hvile.
- Bemærk, at accelerationen på grund af tyngdekraften på jordens overflade altid er konstant: g = 9,8 m/s2
- Eksempel: vægt = m * g = 4, 2 * 9, 8 = 41, 16

Trin 4. Skriv dine svar ned
Det foregående trin vil løse problemet og give dig dit svar.
Eksempel: Den normale kraft er 41, 16 N
Metode 2 af 5: Normal kraft på et skråt plan
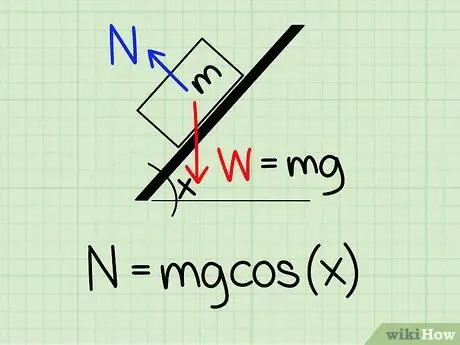
Trin 1. Brug den korrekte ligning
For at beregne den normale kraft på et objekt, der vippes af en bestemt vinkel, skal du bruge formlen: N = m * g * cos (x)
- For denne ligning, N symboliserer normal stil, m repræsenterer objektets masse g repræsenterer accelerationen på grund af tyngdekraften, og x repræsenterer den skrå vinkel.
- Eksempel: Find den normale kraft af en blok med en masse på 4,2 kg, som hviler på et skråt plan med en hældning på 45 grader.

Trin 2. Find cosinus for vinklen
Vinklenes cosinus er lig med sinus for den komplementære vinkel eller den tilstødende side divideret med hypotenusen i trekanten dannet af hældningen.
- Denne værdi bestemmes ofte med en lommeregner, fordi cosinus for enhver vinkel altid er konstant, men du kan også beregne den manuelt.
- Eksempel: cos (45) = 0,71
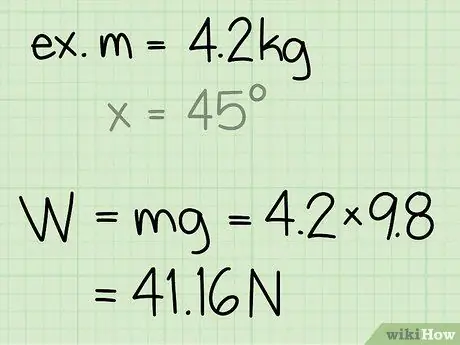
Trin 3. Find objektets vægt
Objektets vægt er lig med objektets masse gange accelerationen på grund af tyngdekraften.
- Bemærk, at accelerationen på grund af tyngdekraften på jordens overflade altid er konstant: g = 9,8 m/s2
- Eksempel: vægt = m * g = 4, 2 * 9, 8 = 41, 16
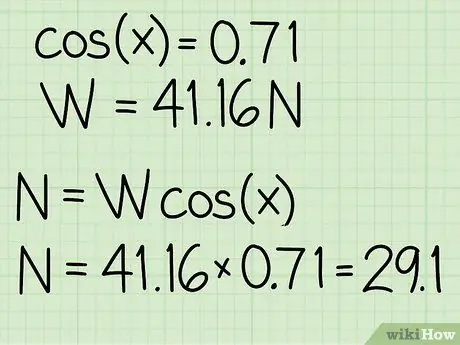
Trin 4. Multiplicer de to værdier
For at finde den normale kraft skal du gange objektets vægt med cosinus i hældningsvinklen.
Eksempel: N = m * g * cos (x) = 41, 16 * 0, 71 = 29, 1
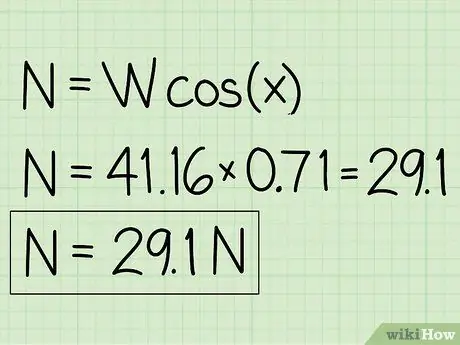
Trin 5. Skriv dine svar ned
Det foregående trin løser problemet og giver dit svar.
- Bemærk, at når et objekt hviler på en skråning, vil den normale kraft være mindre end objektets vægt.
- Eksempel: Den normale kraft er 29,1 N.
Metode 3 af 5: Normal stil med ydre ned -stil
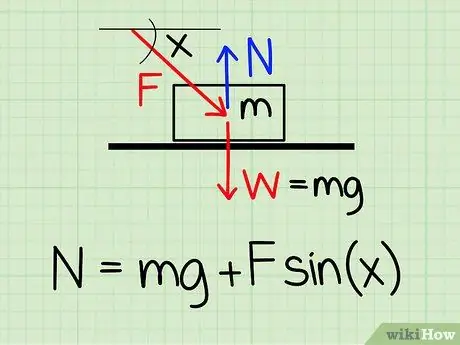
Trin 1. Brug den korrekte ligning
For at beregne den normale kraft på et objekt i hvile, hvis der er en ekstern nedadgående kraft på objektet, skal du bruge ligningen: N = m * g + F * sin (x) '
- N symboliserer normal stil, m repræsenterer objektets masse g repræsenterer accelerationen på grund af tyngdekraften, F symboliserer ekstern stil, og x repræsenterer vinklen mellem objektet og retningen af den ydre kraft.
- Eksempel: Find den normale kraft af et objekt med en masse på 4,2 kg, hvis objektet skubbes af en person i en vinkel på 30 grader og en kraft på 20,9 N.
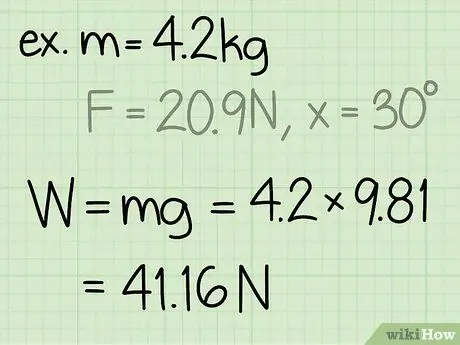
Trin 2. Find objektets vægt
Objektets vægt er lig med objektets masse gange accelerationen på grund af tyngdekraften.
- Bemærk, at accelerationen på grund af tyngdekraften på jordens overflade altid er konstant: g = 9,8 m/s2
- Eksempel: vægt = m * g = 4, 2 * 9, 8 = 41, 16
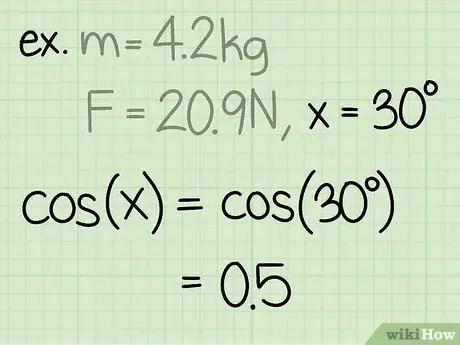
Trin 3. Find sinus for vinklen
Sinus for en vinkel beregnes ved at dividere siden af trekanten modsat vinklen med vinkelens hypotenuse.
Eksempel: sin (30) = 0,5

Trin 4. Gang sinus med den ydre kraft
Ekstern kraft, i dette eksempel, refererer til den nedadgående kraft, der rammer objektet.
Eksempel: 0, 5 * 20, 9 = 10, 45
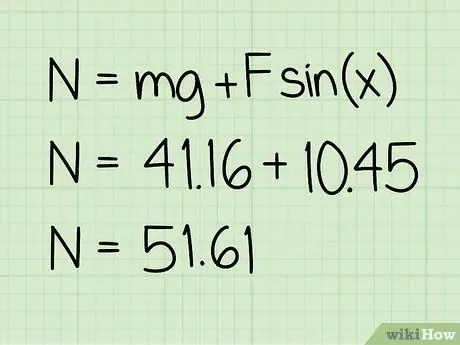
Trin 5. Tilføj denne værdi til vægten
Denne sum vil give størrelsen af den normale kraft, der virker.
Eksempel: 10, 45 + 41, 16 = 51, 61
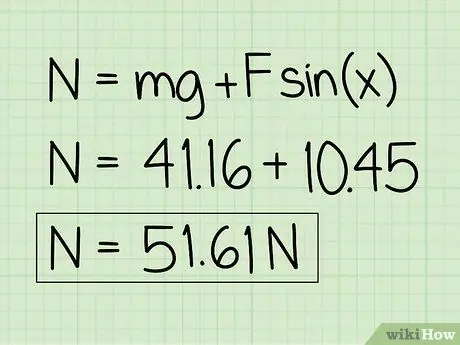
Trin 6. Skriv dine svar ned
Bemærk, at for et objekt i hvile, der påvirkes af en ekstern nedadgående kraft, vil den normale kraft være større end objektets vægt.
Eksempel: Den normale kraft er 51,61 N
Metode 4 af 5: Normal stil med ydre stil op
Trin 1. Brug den korrekte ligning
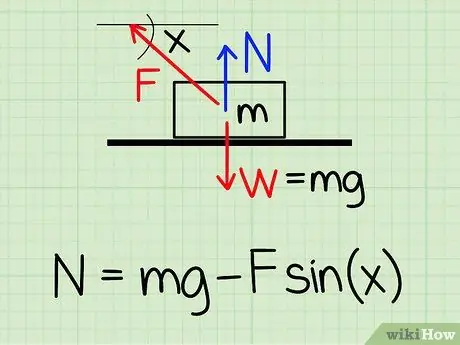
For at beregne den normale kraft på et objekt i hvile, hvis der er en ekstern opadgående kraft på objektet, skal du bruge ligningen: N = m * g - F * sin (x) '
- N symboliserer normal stil, m repræsenterer objektets masse g repræsenterer accelerationen på grund af tyngdekraften, F symboliserer ekstern stil, og x repræsenterer vinklen mellem objektet og retningen af den ydre kraft.
- Eksempel: Find den normale kraft af en blok med en masse på 4,2 kg, hvis nogen trækker blokken op i en vinkel på 50 grader og en kraft på 20,9 N.

Trin 2. Find objektets vægt
Objektets vægt er lig med objektets masse gange accelerationen på grund af tyngdekraften.
- Bemærk, at accelerationen på grund af tyngdekraften på jordens overflade altid er konstant: g = 9,8 m/s2
- Eksempel: vægt = m * g = 4, 2 * 9, 8 = 41, 16
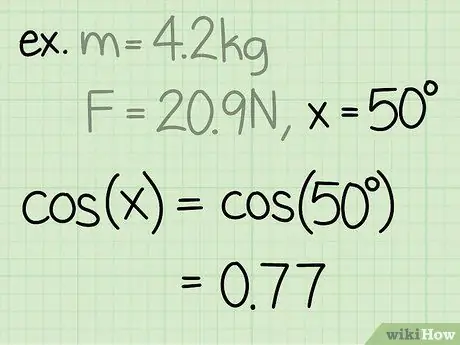
Trin 3. Find sinus for vinklen
Sinus for en vinkel beregnes ved at dividere siden af trekanten modsat vinklen med vinkelens hypotenuse.
Eksempel: sin (50) = 0, 77

Trin 4. Gang sinus med den ydre kraft
Ekstern kraft refererer til den opadgående kraft, der rammer objektet, i dette tilfælde.
Eksempel: 0,77 * 20, 9 = 16, 01
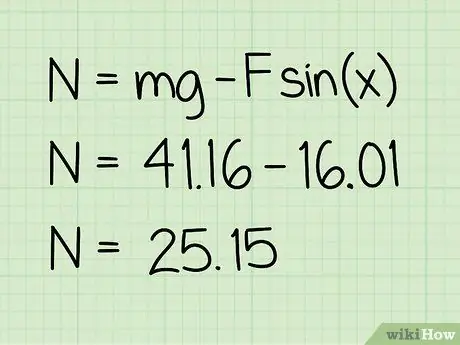
Trin 5. Træk denne værdi fra vægten
Den subtraktion, du gør, vil give dig størrelsen af den normale kraft, der virker på den.
Eksempel: 41, 16 - 16, 01 = 25, 15
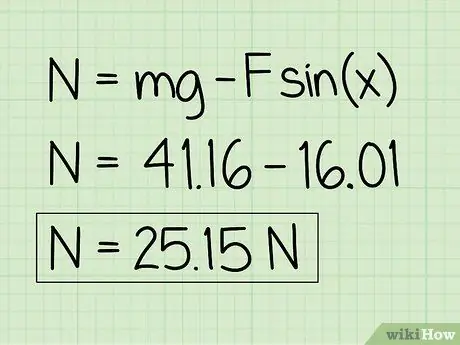
Trin 6. Skriv dine svar ned
Bemærk, at et objekt i hvile påvirkes af en opadgående ydre kraft, den normale kraft vil være mindre end objektets vægt.
Eksempel: Den normale kraft er 25, 15 N
Metode 5 af 5: Normal kraft og friktion

Trin 1. Kend den grundlæggende ligning for kinetisk friktion
Kinetisk friktion eller friktion af et objekt i bevægelse er lig med friktionskoefficienten gange den normale kraft af et objekt. I ligningsform: f = * N
- I denne ligning, f symboliserer friktion, ️ repræsenterer friktionskoefficienten, og N repræsenterer objektets normale kraft.
- "Friktionskoefficienten" er forholdet mellem friktionskraften og den normale kraft, som komprimerer to modstående overflader.
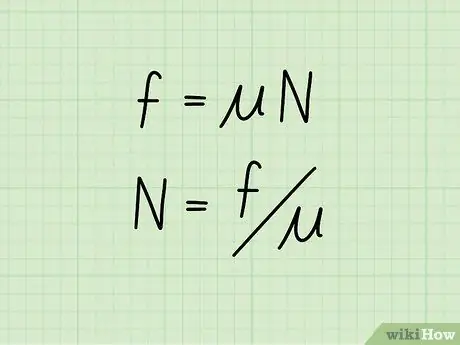
Trin 2. Konfigurer ligningen for at isolere den normale kraft
Hvis du kender værdien af et objekts kinetiske friktion såvel som dets friktionskoefficient, kan du beregne den normale kraft ved hjælp af formlen: N = f /
- Begge sider af den oprindelige ligning er divideret med ️, hvorved den normale kraft isoleres på den ene side, mens friktionskoefficienten og kinetisk friktion beregnes på den anden.
- Eksempel: Find en bloks normale kraft, hvis friktionskoefficienten er 0,4, og størrelsen af den kinetiske friktion er 40 N.
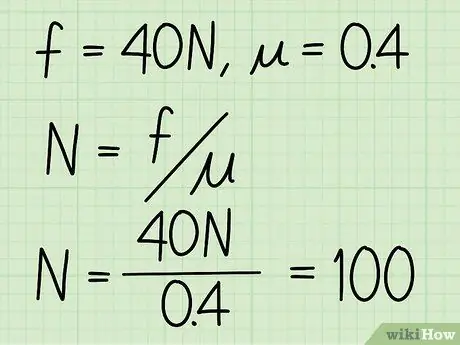
Trin 3. Divider den kinetiske friktion med friktionskoefficienten
Grundlæggende er dette alt hvad du skal gøre for at finde størrelsen af den normale kraft.
Eksempel: N = f / = 40/0, 4 = 100
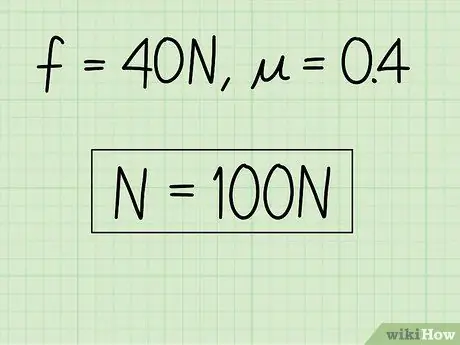
Trin 4. Skriv dine svar ned
Hvis det ønskes, kan du kontrollere dit svar ved at sætte det tilbage i den originale ligning for kinetisk friktion. Hvis du ikke vil have det, har du løst problemet.