Tyngdekraften er en af de grundlæggende kræfter i fysikken. Det vigtigste aspekt af tyngdekraften er, at den er universel: alle objekter har en tyngdekraft, der tiltrækker andre genstande. Tyngdekraftens størrelse afhænger af massen og afstanden mellem de to objekter.
Trin
Del 1 af 2: Beregning af tyngdekraften mellem to objekter

Trin 1. Definer ligningen for tyngdekraften, der trækker på et objekt, Fgrav = (Gm1m2)/d2.
For at kunne beregne et objekts tyngdekraft tager denne ligning også hensyn til masserne af de to objekter og deres afstand til hinanden. Ligningsvariablerne er beskrevet nedenfor.
- Fgrav er tyngdekraften
- G er den universelle gravitationskonstant 6.673 x 10-11 Nm2/kg2
- m1 er massen af det første objekt
- m2 er massen af det andet objekt
- d er afstanden mellem midten af de to objekter
- Nogle gange finder du bogstavet r i stedet for d. Disse to symboler repræsenterer afstanden mellem de to objekter.

Trin 2. Brug de relevante metriske enheder
Til denne ligning skal du bruge metriske enheder. Objektets masse skal være i kilogram (kg), og afstanden mellem genstandene skal være i meter (m). Du skal konvertere disse enheder til metriske enheder, før du fortsætter

Trin 3. Bestem massen af det pågældende objekt
For små genstande kan du veje dem for at bestemme deres vægt i kilogram. For store objekter kan du slå den omtrentlige masse op på et bord eller på internettet. I fysikproblemer vil normalt objektets masse blive fortalt.

Trin 4. Mål afstanden mellem de to objekter
Hvis du forsøger at beregne tyngdekraften mellem et objekt og jorden, skal du vide, hvor langt dette objekt er fra midten af jorden.
- Afstanden fra jordens overflade til midten af jorden er omkring 6,38 x 106 m.
- Du kan slå tabeller eller andre kilder op på internettet, der fortæller dig den omtrentlige afstand fra midten af jorden til objekter i forskellige højder på jordens overflade.

Trin 5. Afslut beregningen
Hvis du har defineret variablerne i ligningen, er du velkommen til at indtaste dem for at løse. Sørg for, at alle variabler er i metriske enheder og er korrekt skaleret. Massen skal være i kilogram, og afstanden skal være i meter. Løs ligninger i den korrekte rækkefølge af beregninger.
- Bestem f.eks. Tyngdekraften for en person, hvis masse er 68 kg over jordens overflade. Jordens masse er 5,98 x 1024 kg.
- Sørg for, at alle variabler er i korrekte enheder. m1 = 5, 98 x 1024 kg, m2 = 68 kg, G = 6.673 x 10-11 Nm2/kg2og d = 6, 38 x 106 m
- Skriv din ligning: Fgrav = (Gm1m2)/d2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)]/(6, 38 x 106)2
- Gang masserne af de to objekter, der tages i betragtning. 68 x (5, 98 x 1024) = 4,06 x 1026
- Multiplicer resultatet m1 og m2 med gravitationskonstanten G. (4,06 x 1026) x (6,67 x 10-11) = 2.708 x 1016
- Kvadratér afstanden mellem de to objekter. (6, 38 x 106)2 = 4,07 x 1013
- Delresultat G x m1 x m2 med afstanden i kvadrat for at opnå tyngdekraften i Newton (N). 2, 708 x 1016/4, 07 x 1013 = 665 N
- Dens tyngdekraft er 665 N.
Del 2 af 2: Beregning af tyngdekraften på jorden

Trin 1. Forstå Newtons anden lov, F = ma
Newtons anden lov siger, at accelerationen af et objekt er direkte proportional med nettokraften, der virker på det og omvendt proportional med dets masse. Med andre ord, hvis en kraft, der virker på et objekt, er større end den kraft, der virker i den modsatte retning, vil objektet bevæge sig med den stærkere kraft.
- Denne lov kan opsummeres ved ligningen F = ma, hvor F er kraften, m er objektets masse, og a er accelerationen.
- Takket være denne lov kan vi beregne tyngdekraften for alle objekter på jordens overflade ved hjælp af den kendte acceleration på grund af tyngdekraften.
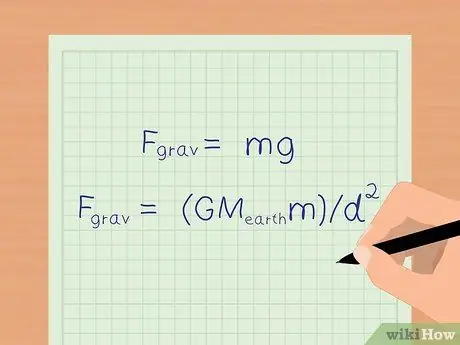
Trin 2. Find accelerationen på grund af Jordens tyngdekraft
På jorden får tyngdekraften alle objekter til at accelerere med 9,8 m/s2. På jordoverfladen kan vi bruge en forenklet ligning: Fgrav = mg for at beregne tyngdekraften.
Hvis du vil vide et mere præcist antal tyngdekræfter, kan du stadig bruge formlen i det foregående trin, Fgrav = (GMjordenm)/d2 at bestemme tyngdekraften.

Trin 3. Brug de relevante metriske enheder
Til denne ligning skal du bruge metriske enheder. Objektets masse skal være i kilogram (kg), og afstanden mellem genstandene skal være i meter (m). Du skal konvertere disse enheder til metriske enheder, før du fortsætter.

Trin 4. Bestem massen af det pågældende objekt
For små genstande kan du veje dem for at bestemme deres vægt i kilogram. For store objekter kan du slå den omtrentlige masse op på et bord eller på internettet. I fysikproblemer vil normalt objektets masse blive fortalt.

Trin 5. Afslut beregningen
Hvis du har defineret variablerne i ligningen, er du velkommen til at indtaste dem for at løse. Sørg for, at alle variabler er i metriske enheder og er korrekt skaleret. Massen skal være i kilogram, og afstanden skal være i meter. Løs ligninger i den korrekte rækkefølge af beregninger.
- Lad os prøve at bruge ligningen i det foregående trin og se, hvor tæt resultaterne er. Bestem tyngdekraften for en person med en masse på 68 kg på jordens overflade.
- Sørg for, at alle variabler er i korrekte enheder: m = 68 kg, g = 9,8 m/s2.
- Skriv formlen ned. Fgrav = mg = 68*9, 8 = 666 N.
- Ved hjælp af formlen F = mg er tyngdekraften 666 N, mens resultatet fra formlen i det foregående trin er 665 N. Som du kan se, er de to resultater næsten ens.
Tips
- Disse to formler skulle give det samme svar, men den kortere og enklere formel er lettere at bruge, når man diskuterer objekter på overfladen af en planet.
- Brug den første formel, hvis du ikke kender accelerationen på grund af tyngdekraften på en planet, eller hvis du beregner tyngdekraften mellem to meget store objekter, såsom månen eller planeter.







