Subtraktion er ganske enkelt at trække et tal fra et andet. Det er let at trække et helt tal fra et andet, men subtraktion kan være vanskelig, hvis du trækker brøk eller decimaler. Når du forstår subtraktion, vil du være i stand til at bruge mere komplekse matematiske begreber og lettere kunne tilføje, multiplicere og dividere tal.
Trin
Metode 1 af 6: Fratrækning af store tal ved låntagning

Trin 1. Skriv et stort antal ned
For eksempel vil du løse 32 - 17. Skriv 32 først ned.

Trin 2. Skriv det mindre tal lige under det
Sørg for, at du placerer værdierne tiere og enere i de korrekte kolonner, så 3 af 32 er direkte over 1 af 17 og 2 af 32 er direkte over 7 af 17.
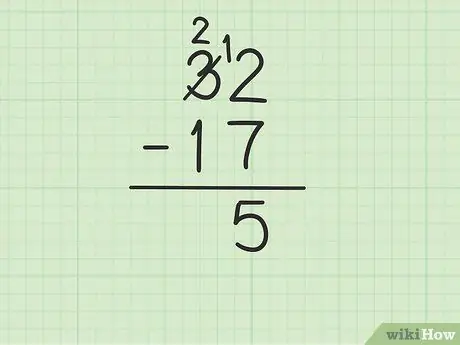
Trin 3. Træk det øverste tal i kolonnen enheder fra tallet nederst
Dette kan dog blive kompliceret, hvis bundnummeret er større end det øverste tal. I dette tilfælde er 7 større end 2. Her er hvad du skal gøre:
- Du skal låne fra nummer 3 på 32 (også kendt som gruppering) for at gøre 2 til 12.
- Kryds nummer 3 ud af 32 og erstat det med nummer 2, mens tallet 2 bliver 12.
- Nu kan du trække 12 - 7, hvilket svarer til 5. Skriv 5 under de to tal, du trækker fra, så de er i enhedskolonnen i den nye række.
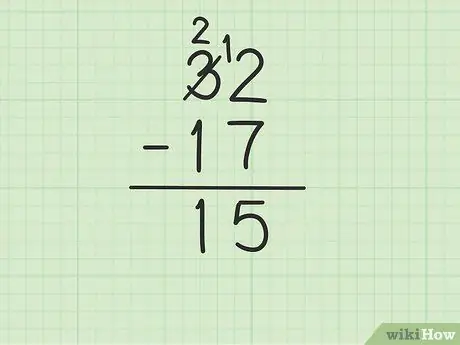
Trin 4. Træk det øverste tal i kolonnen tiere fra det nederste tal
Husk 3 er blevet til 2. Træk nu 1 fra 17 fra 2 ovenfor for at få (2-1) 1. Skriv 1 nedenfor, i tierkolonnen, til venstre for 5 i kolonnen enheder. Du skriver 15. Det vil sige 32 - 17 = 15.
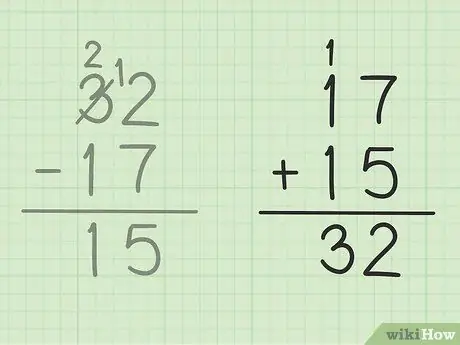
Trin 5. Kontroller dit arbejde
Hvis du vil sikre dig, at du har trukket to tal korrekt fra, skal du blot tilføje dit svar med det mindre tal for at lave et stort tal. I dette problem skal du tilføje dit svar, 15 til det mindre antal subtraktion, 17. 15 + 17 = 32, så dit svar er korrekt. Sikker!
Metode 2 af 6: Træk små hele tal fra
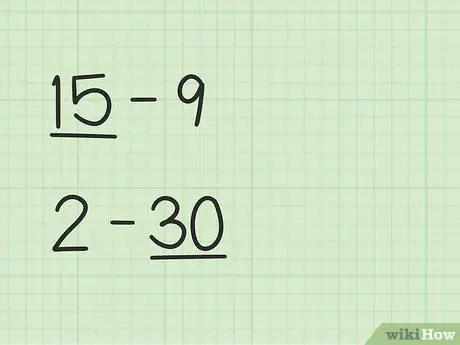
Trin 1. Find det større tal
Problemer som 15 -9 vil have en anden måde end 2 -30.
- I spørgsmål 15 - 9 er det første tal, 15, større end det andet tal, 9.
- I spørgsmål 2 - 30 er det andet tal, 30, større end det første tal, 2.
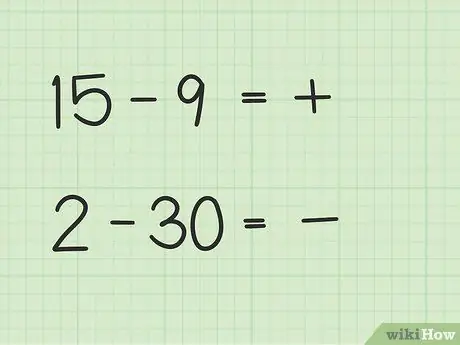
Trin 2. Beslut, om dit svar vil være positivt eller negativt
Hvis det første tal er større, er svaret positivt. Hvis det andet tal er større, er svaret negativt.
- I det første spørgsmål, 15 - 9, er dit svar positivt, fordi det første tal er større end det andet tal.
- I det andet spørgsmål, 2 - 30, er dit svar negativt, fordi det andet tal er større end det første tal.
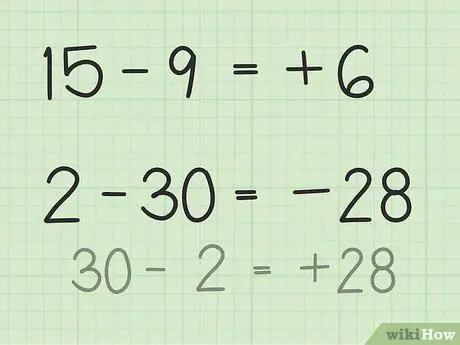
Trin 3. Find forskellen mellem to tal
For at trække to tal fra skal du forestille dig forskellen mellem de to tal og beregne tallene mellem dem.
- For spørgsmål 15 - 9, forestil dig en stak med 15 pokerchips. Kast 9 chips og kun 6. Så, 15 - 9 = 6. Du kan også forestille dig en talelinje. Tænk på tallene fra 1 til 15, kassér eller returner 9 enheder, så du får 6.
- For spørgsmål 2 - 30 er den nemmeste måde at løse dette på at invertere tallet og gøre resultatet negativt efter at trække fra. Så 30 - 2 = 28, så 28 og 30 har en forskel på 2. Gør nu resultatet negativt, fordi du allerede har fastslået, at svaret er negativt, fordi det andet tal er større end det første tal. Så 2 -30 = -28.
Metode 3 af 6: Træk decimaler
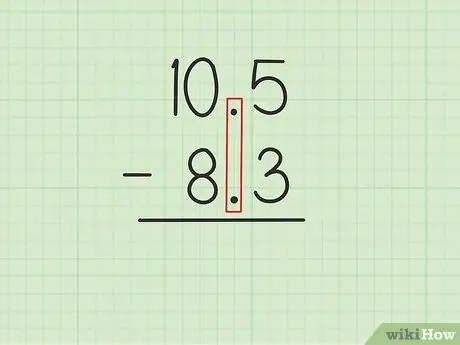
Trin 1. Skriv det større tal over det mindre tal med decimaltegnene justeret
Antag, at du vil løse følgende problemer: 10, 5 - 8, 3. Skriv 10, 5 over 8, 3, så decimaltegnene for de to tal er parallelle., 5 af 10, 5 skal være direkte over, 3 af 8, 3 og 0 af 10, 5 skal være over 8 af 8, 3.
Hvis du har et problem, fordi de to tal ikke har det samme tal efter decimalpunktet, skal du skrive 0 i tomrummet, indtil summen af tallene er den samme. For eksempel er problemet 5, 32 - 4, 2, du kan skrive det som 5, 32 - 4, 2 0. Dette ændrer ikke værdien af det andet tal, men gør det lettere at trække de to tal fra.

Trin 2. Træk det øverste tal i kolonnen tiere fra tallet nedenfor
I dette tilfælde skal du trække 3 fra 5. 5 - 3 = 2, så du skal skrive 2 under 3 af 8, 3.
Sørg for at sætte et decimaltegn i svaret, så det er skrevet 2

Trin 3. Træk tallet over kolonnen enheder fra tallet under det
Du skal trække 8 fra 0. Lån 1 fra tiendedelen for at ændre 0 til 10 og trække 10 - 8 for at få 2. Du kan også tælle 10 - 8 uden at låne, fordi der ikke er tal i den anden tiers kolonne. Skriv svaret under 8, til venstre for decimaltegnet.

Trin 4. Skriv dit endelige resultat ned
Dit endelige resultat er 2, 2.

Trin 5. Kontroller dit arbejde
Hvis du vil sikre dig, at din decimalfradrag er korrekt, skal du blot tilføje dit svar med det mindre tal for at få det større tal. 2, 2 + 8, 3 = 10, 5, så du er færdig.
Metode 4 af 6: Træk fraktioner fra

Trin 1. Juster brøkerens nævner og tæller
Antag, at du vil løse problemer 13/10 - 3/5. Skriv problemet, så de to tællere, 13 og 3 og de to nævnere, 10 og 5 er modsat hinanden. Disse to tal adskilles med et subtraktionstegn. Dette hjælper dig med at visualisere problemet og løse det lettere.

Trin 2. Find den mindst fællesnævner
Den mindst fællesnævner er det mindste tal, der kan divideres med to tal. I dette eksempel skal du finde den mindste fællesnævner, der kan deles med 10 og 5. Du finder, at 10 er den mindste fællesnævner for begge tal, fordi 10 er delelig med 10 og 5.
Bemærk, at den mindst fællesnævner af to tal ikke altid er et af dem. For eksempel er den mindste fællesnævner for 3 og 2 6, fordi 6 er det mindste tal, der kan divideres med to tal
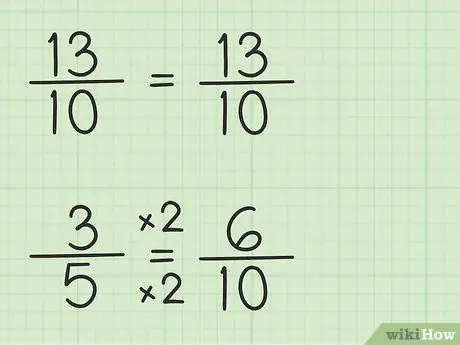
Trin 3. Skriv brøkerne ned ved hjælp af den samme nævner
Brøken 13/10 kan skrives på samme måde, fordi nævneren er 10, den mindste fællesnævner, som er 10, gange 1. Imidlertid skal brøken 3/5 omskrives, fordi nævneren er 5, den mindste fællesnævner, som er 10, gange 2. Så brøken 3/5 skal ganges med 2/2 for at gøre nævneren 10, så 3/5 x 2/2 = 6/10. Du har fundet den tilsvarende brøk. 3/5 svarer til 6/10, selvom 6/10 giver dig mulighed for at trække det første tal, 13/10.
Skriv et nyt spørgsmål som dette: 13/10 - 6/10
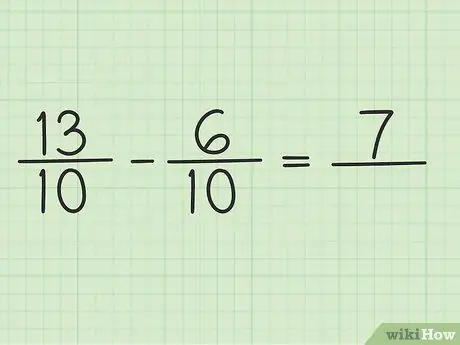
Trin 4. Træk tælleren til to tal
Træk blot 13 - 6, så resultatet er 7. Du kan ikke ændre nævneren for brøken.
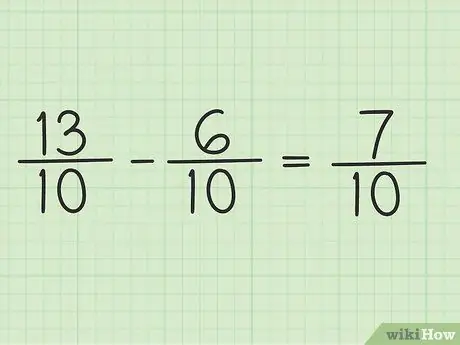
Trin 5. Skriv den nye tæller over den samme nævner for at få det endelige resultat
Den nye tæller er 7. Begge brøker har en nævner på 10. Dit endelige resultat er 7/10.
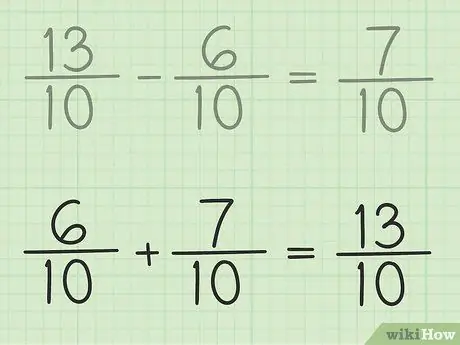
Trin 6. Kontroller dit arbejde
Hvis du vil sikre dig, at du trækker fraktionen korrekt, skal du blot tilføje dit svar og den mindre brøk, så resultatet er en større brøk. 7/10 + 6/10 = 13/10. Det er færdigt.
Metode 5 af 6: Træk fraktioner fra hele tal

Trin 1. Skriv problemet ned
Antag f.eks., At du vil løse følgende problem: 5 -. Skriv det ned.
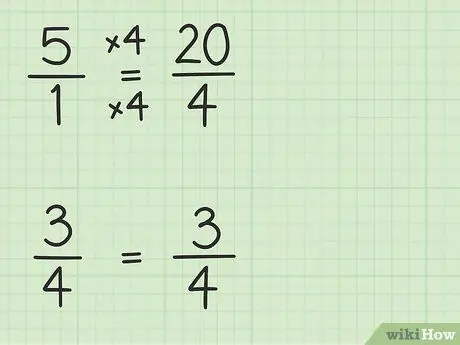
Trin 2. Konverter hele tal til brøker, der har samme nævner som andre brøker
Du konverterer 5 til en brøkdel med en nævner på 4 for at kunne trække to tal fra. Så du skal tænke på 5 som en brøkdel af 5/1. Derefter kan du gange den nye brøk tæller og nævner med 4 for at gøre de to tal nævnere de samme. Så 5/1 x 4/4 = 20/4. Denne brøk er lig med 5, men giver dig mulighed for at trække to tal fra.
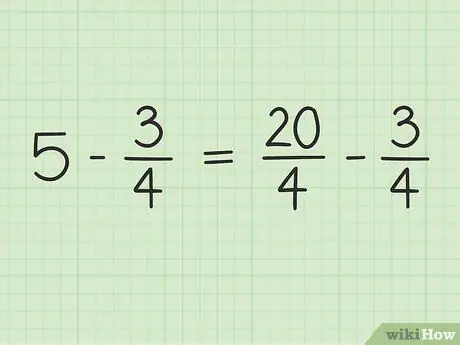
Trin 3. Omskriv problemet
Det nye problem kan skrives sådan: 20/4 - 3/4.
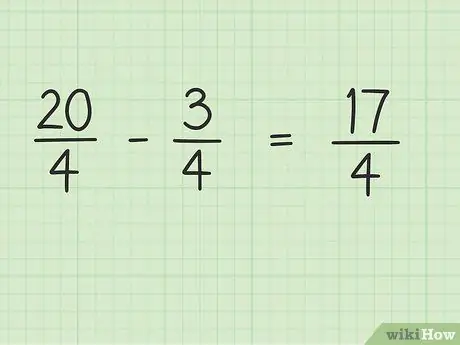
Trin 4. Træk tælleren for brøken, mens nævneren forbliver den samme
Træk nu bare 20 x 3 for at få det endelige resultat. 20 - 3 = 17, så 17 er den nye tæller. Du kan efterlade nævneren den samme.
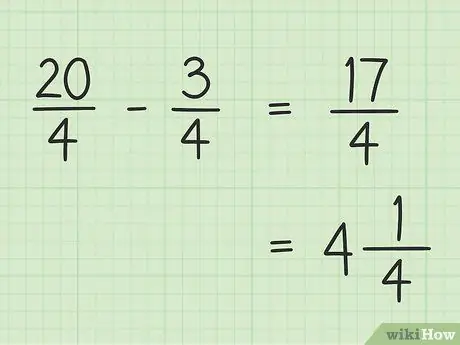
Trin 5. Skriv dit endelige resultat ned
Dit endelige resultat er 17/4. Hvis du vil skrive det som et blandet tal, dividerer du 17 med 4, så resultatet er 4, og resten er 1, så din sidste 17/4 er lig med 4.
Metode 6 af 6: Subtrahering af variabler
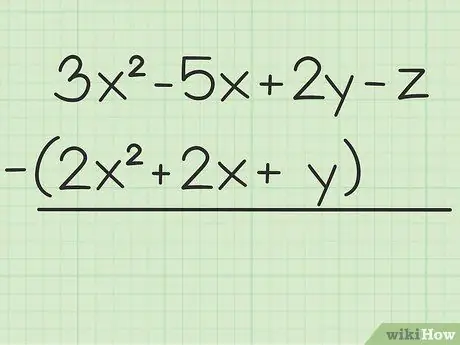
Trin 1. Skriv ned det problem, du vil løse
For eksempel følgende spørgsmål: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Skriv det første sæt variabler over det andet.
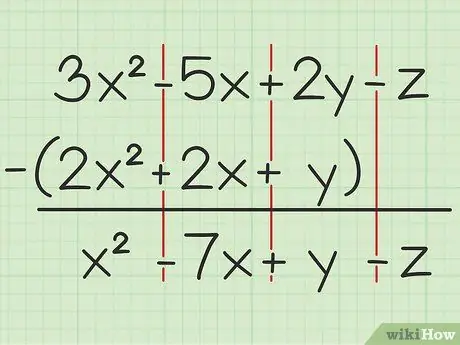
Trin 2. Træk de samme variabler fra
Hvis du støder på en variabel, kan du kun tilføje eller fratrække den samme variabel, og som er skrevet med samme grad af kvadrat. Det betyder, at du kan trække 4x fra2 fra 7x2, men kan ikke trække 4x fra 4y. Så du kan opdele problemet sådan:
- 3x2 - 2x2 = x2
- -5x -2x = -7x
- 2y - y = y
- -z -0 = -z
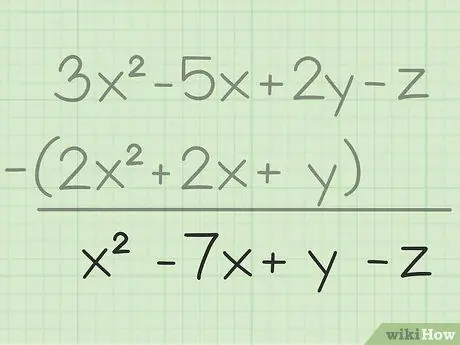
Trin 3. Skriv dit endelige resultat ned
Du har trukket alle de samme variabler, alt du skal gøre er at skrive dit endelige resultat, som vil indeholde alle de variabler, du har trukket fra. Her er slutresultatet:







