Studerende, der stadig er meget unge, har ofte svært ved at forstå begrebet subtraktion. Hvis du er lærer og ønsker at undervise begrebet subtraktion til elever, så prøv at repræsentere konceptet på en måde, der er interessant og mere forståelig for eleverne. Efter at have forklaret de grundlæggende begreber for subtraktion, kan du prøve at gå videre til begrebet tocifret subtraktion. Når eleverne har mestret det godt, kan du prøve at forklare forskellige begreber, de kan bruge til at løse subtraktionsproblemer, såsom Common Core.
Trin
Metode 1 af 4: Undervisning i subtraktion gennem objekter eller billeder

Trin 1. Skriv eller præsenter mundtligt et historieproblem med et subtraktionsproblem for eleverne:
Der er 8 appelsiner på bordet, 3 appelsiner spises af Jordan. Hvor mange appelsiner er der tilbage?
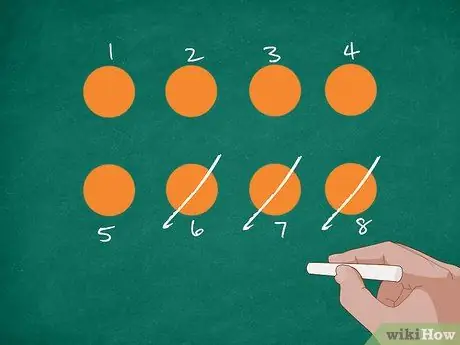
Trin 2. Repræsentér problemet med billeder
Først tegner du 8 orange cirkler på tavlen eller et stykke papir. Lad derefter eleverne tælle tallet og mærke hver cirkel med et tal. Streg 3 cirkler ud, mens du forklarer, at Jordan spiste 3 appelsiner. Spørg eleverne, hvor mange appelsiner der nu er tilbage.
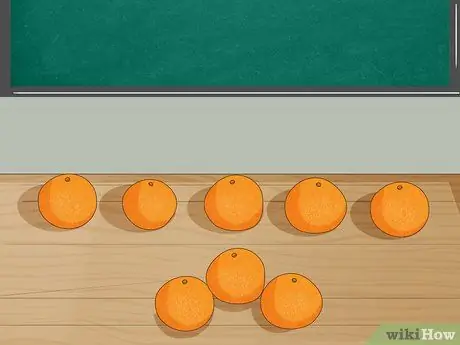
Trin 3. Repræsentér problemet med objekter
Læg 8 appelsiner på bordet og bed eleverne om at tælle tallet. Tag derefter 3 appelsiner fra bordet, mens du forklarer, at Jordan spiste 3 appelsiner. Lad eleverne tælle antallet af resterende appelsiner.

Trin 4. Skriv ligningen ned
Forklar, at historieproblemer også kan repræsenteres gennem en ligning. Sørg for, at du altid guider dem i processen med at omdanne historieproblemer til matematiske ligninger.
- Spørg, hvor mange appelsiner der er på bordet. Skriv tallet "8" på tavlen.
- Spørg, hvor mange appelsiner Jordan spiste. Skriv tallet "3" på tavlen.
- Spørg eleverne, om dette er et additions- eller subtraktionsproblem. Skriv et “-” tegn mellem tallene “8” og “3”.
- Lad eleverne lede efter svar på ligningen "8-3". Skriv et “=” tegn efterfulgt af tallet “5.”
Metode 2 af 4: Undervisning af subtraktion med nedtællingsmetoden på tallinjen

Trin 1. Skriv eller præsenter mundtligt et historieproblem med et subtraktionsproblem for eleverne:
Der er 10 hunde i dyrebutikken, hvoraf 6 er blevet adopteret af deres nye ejere. Hvor mange hunde er der tilbage i dyrebutikken?
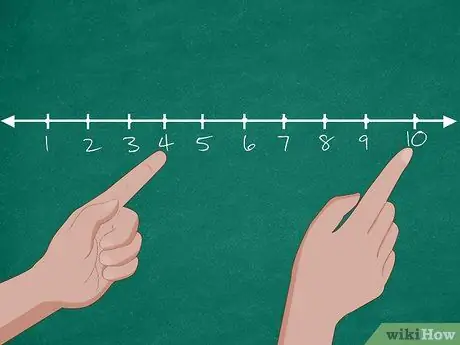
Trin 2. Brug hjælp af en talelinje til at løse problemet
Først tegner du en talelinje, der indeholder tallene 0-10 på tavlen. Bed derefter eleverne om at navngive antallet af hunde i dyrebutikken. Når eleverne har svaret, skal du cirkulere tallet "10" på tavlen. Spørg derefter igen, hvor mange hunde der er blevet adopteret. Hvis eleverne svarer "6", bed dem om at tælle 6 tal ned fra 10 (9, 8, 7, 6, 5, 4), indtil de når tallet "4". Spørg derefter igen, hvor mange hunde der er tilbage i dyrebutikken.

Trin 3. Skriv ligningen ned
Forklar, at historieproblemer også kan repræsenteres gennem en ligning. Sørg for, at du altid guider dem i processen med at omdanne historieproblemer til matematiske ligninger.
- Spørg, hvor mange hunde der er i dyrebutikken. Skriv tallet "10" på tavlen.
- Spørg, hvor mange hunde der blev adopteret. Skriv tallet "6" på tavlen.
- Spørg eleverne, om dette er et additions- eller subtraktionsproblem. Skriv et “-” tegn mellem tallene “10” og “6”.
- Lad eleverne lede efter svar på ligningen "10-6". Skriv et “=” tegn efterfulgt af tallet “4.”
Metode 3 af 4: Undervisning i subtraktion gennem faktafamiliekoncepter

Trin 1. Introducer begrebet faktafamilie for studerende
Faktisk er en faktafamilie en gruppe af matematiske problemer, der består af de samme tal. For eksempel danner tallene 10, 3 og 7 en faktafamilie. De tre tal kan tilføjes eller trækkes fra på forskellige måder; Du kan generere to ligninger ved hjælp af kun disse 3 tal:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

Trin 2. Skriv eller præsenter verbalt et historisk problem, der indeholder et subtraktionsproblem, for eleverne:
Jeg har 7 slik. Hvis jeg spiser 3 slik, hvor mange slik er der tilbage?

Trin 3. Brug faktafamiliekonceptet til at løse problemet
Vejled eleverne gennem processen trin for trin:
- Spørg eleverne, hvilket problem de gerne vil løse. Skriv "7-3 =?" på tavlen.
- Bed dem om at identificere det tredje medlem af faktafamiliegruppen. Skriv følgende ligninger på tavlen: “3+_ = 7”; “_+3 = 7”; "; “7 -_ = 3”; og 7-3 = _”Bed derefter eleverne om at læse resultaterne og udfylde problemet med de svar, de gav.
Metode 4 af 4: Introduktion til fælles kernekoncepter
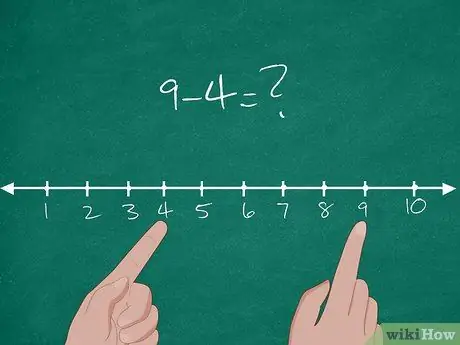
Trin 1. Lær begrebet subtraktion i Common Core
Faktisk er Common Core en ny læringsstandard, der anvendes af de fleste stater i Amerika. I Common Core forklares det grundlæggende koncept med subtraktion af afstanden mellem to tal. For at forklare konceptet for eleverne, prøv at tegne en talelinje, der indeholder tallene 1-10 på tavlen.
- Giv derefter et grundlæggende subtraktionsproblem til eleverne: 9-4 = ?.
- Find placeringen af tallet 4 på tallinjen. Forklar for eleverne, at denne placering er deres udgangspunkt.
- Find placeringen af tallet 9 på tallinjen. Forklar for eleverne, at placeringen er den endelige destination.
- Bed derefter eleverne om at måle eller beregne afstanden mellem de to tal: "5, 6, 7, 8, 9."
- Afstanden mellem de to tal er 5. Således er 9-4 = 5.
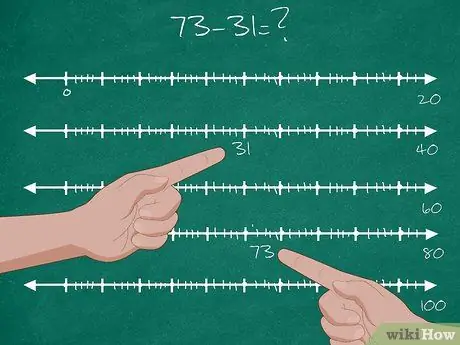
Trin 2. Lad eleverne løse det tocifrede subtraktionsproblem
Forklar for eleverne, at der vil være to punkter, de skal stoppe, før de ankommer til deres destination.
- Giv eleverne et tocifret subtraktionsproblem: 73-31 = ?.
- Find placeringen af tallet 31 på tallinjen. Dette er udgangspunktet.
- Find placeringen af tallet 73 på tallinjen. Dette er slutmålet.
- “Stop” ved den første tiende efter 31. Således er dit første stop 40. Mål derefter afstanden mellem 31 og 40, og skriv svaret ned: 9.
- "Stop" ved tiendedele, der er tættere på 73. Således er dit andet stop 70. Mål derefter afstanden mellem 40 (første stop) og 70 (andet stop), og skriv svaret ned: 30.
- "Flyt" fra 70 (andet stop) til din endelige destination (73). Mål afstanden mellem dem og skriv svaret ned: 3.
- Tilføj disse tre resultater sammen: 9+30+3 = 42. Således er 73-31 = 42.

Trin 3. Lad eleverne løse det trecifrede subtraktionsproblem
Når du løser tocifrede subtraktionsproblemer, skal du forklare eleverne, at det, der vil stige, ikke kun er mellemlandinger, men også afstanden mellem hvert mellemlanding.
- Giv eleverne et trecifret subtraktionsproblem: 815-398 = ?.
- Find placeringen af tallet 398 på tallinjen. Dette er udgangspunktet.
- Find placeringen af tallet 815 på tallinjen. Dette er slutmålet.
- "Stop" ved den første tiende efter 398. Således er dit første stop 400. Mål afstanden mellem 398 og 400, og skriv svaret ned: 2.
- "Stop" ved de tiendedele, der er tættere på 815. Så dit andet stop er 800. Mål afstanden mellem 400 og 800, og skriv svaret ned: 400.
- "Stop" ved de tiendedele, der er tættere på 815. Således er dit tredje stop 810. Mål afstanden mellem 800 og 810, og skriv svaret ned: 10.
- "Flyt" fra det tredje stop til din endelige destination, som er tallet 815. Mål afstanden, og skriv svaret ned: 5.
- Tilføj alle de tal, du får: 2+400+10+5 = 417. Således 815-398-417.







