Tilføjelse af brøker er en meget nyttig viden. Denne færdighed er meget let at lære og bruge, når man arbejder på matematiske problemer fra folkeskolen til gymnasiet. Denne artikel forklarer, hvordan du tilføjer brøker, så du kan gøre det på få minutter.
Trin
Metode 1 af 2: Tilføjelse af brøker med den samme nævner

Trin 1. Kontroller nævneren (tallet under kvotienten) for hver brøk
Hvis tallene er de samme, tilføjer du brøker med den samme nævner. Hvis nævnerne er forskellige, læs den anden metode.
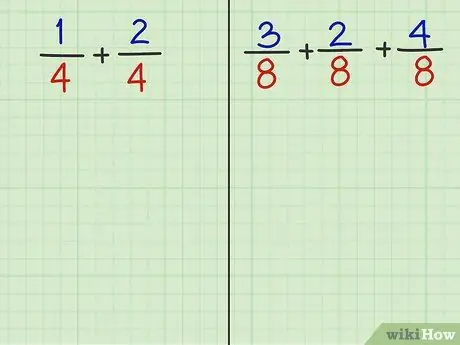
Trin 2. Besvar de følgende 2 spørgsmål
Ved at læse det sidste trin i denne metode, bør du være i stand til at optage brøkdelene af de følgende to spørgsmål.
- Opgave 1: 1/4 + 2/4
- Opgave 2: 3/8 + 2/8 + 4/8
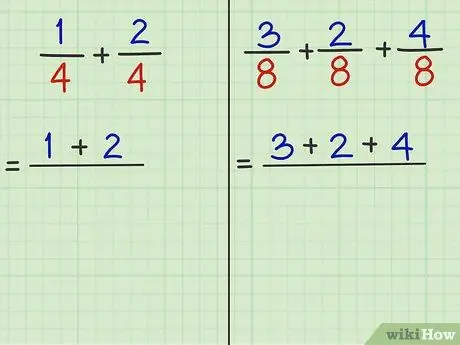
Trin 3. Saml tællerne (tallene over skillelinjen) og tilføj dem
Tælleren er tallet over kvotienten. Uanset hvor mange brøker du vil tilføje, kan du tilføje tællerne med det samme, hvis nævnerne er de samme.
- Opgave 1: 1/4 + 2/4 er den brøkdel, der skal tilføjes. "1" og "2" er tællere. Så 1 + 2 = 3.
- Opgave 2: 3/8 + 2/8 + 4/8 er den brøkdel, der skal tilføjes. "3" og "2" og "4" er tællere. Så 3 + 2 + 4 = 9.

Trin 4. Bestem den nye brøkdel ud fra summen
Skriv tælleren ned i trin 2. Dette tal er ny tæller. Skriv nævneren, som er det samme tal under halvdelen af hver brøk. Du behøver ikke at foretage beregningerne, hvis nævnerne er de samme. Dette nummer er ny nævner og er altid lig med den gamle nævner, når du tilføjer brøker med den samme nævner.
- Opgave 1: 3 er den nye tæller og 4 er den nye nævner. Svaret på spørgsmål 1 er således 3/4. 1/4 + 2/4 = 3/4.
- Opgave 2: 9 er den nye tæller og 8 er den nye nævner. Svaret på spørgsmål 2 er således 9/8. 3/8 + 2/8 + 4/8 = 9/8.
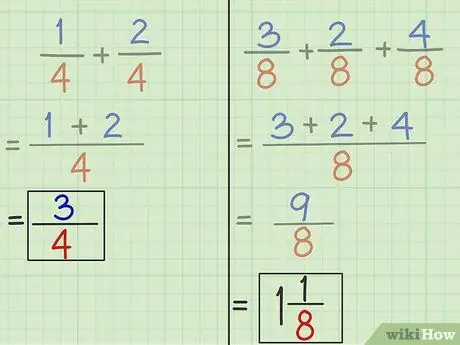
Trin 5. Forenkle fraktioner, hvis det er nødvendigt
Glem ikke at forenkle den nye brøkdel for at gøre det lettere at skrive.
-
Hvis tælleren større i stedet for en nævner som resultatet af tilføjelsen af problem 2, betyder det, at vi får 1 hel måned efter at have forenklet brøken. Divider tælleren med nævneren eller 9 divideret med 8. Resultatet er et heltal 1 tilbage 1. Skriv heltal foran brøken og resten bliver tæller for en ny brøk med samme nævner.
9/8 = 1 1/8.
Metode 2 af 2: Tilføjelse af brøker med forskellige nævnere

Trin 1. Kontroller nævneren (tallet under kvotienten) for hver brøk
Hvis nævnerne er forskellige, er du det tilføj brøker med forskellige nævnere. Læs følgende trin, fordi du skal gøre nævnerne lige, før du tilføjer brøker.
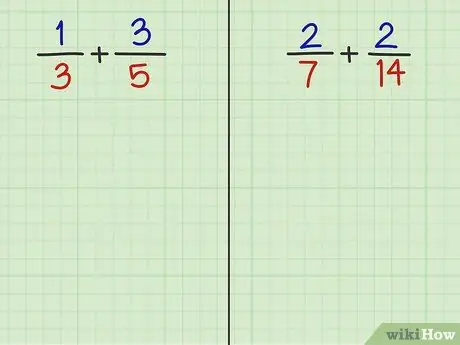
Trin 2. Løs følgende 2 spørgsmål
Ved at læse det sidste trin i denne metode, bør du være i stand til at optage brøkdelene af de følgende to spørgsmål.
- Opgave 3: 1/3 + 3/5
- Spørgsmål 4: 2/7 + 2/14

Trin 3. Match nævnerne
For at gøre dette skal du gange nævnerne for de to fraktioner ovenfor. En let måde at udligne nævnerne på er at gange nævnerne for de to fraktioner. Hvis en af nævnerne er et multiplum af den anden, skal du finde det mindst fælles multiplum af de to nævnere.
-
Opgave 3:
3 x 5 = 15. Så den nye nævner for begge fraktioner er 15.
-
Opgave 4:
14 er et multiplum af 7. Derfor behøver vi kun at gange 7 med 2 for at få 14. Således er den nye nævner for begge fraktioner 14.

Trin 4. Gang tælleren og nævneren for den første brøk med nævneren for den anden brøk
Dette trin ændrer ikke værdien af brøken, men brøken ser ud til at ændre sig for at matche nævneren. Brøkværdien forbliver den samme.
-
Opgave 3:
1/3 x 5/5 = 5/15.
-
Opgave 4:
Til dette problem skal vi bare gange den første brøk med 2/2 for at få nævnerne lige.
2/7 x 2/2 = 4/14

Trin 5. Multiplicer tælleren og nævneren for den anden brøk med nævneren for den første brøk
I lighed med ovenstående trin ændrer vi ikke værdien af brøken, men brøken ser ud til at ændre sig for at udligne nævneren. Brøkværdien forbliver den samme.
-
Opgave 3:
3/5 x 3/3 = 9/15.
-
Opgave 4:
Vi behøver ikke at gange den anden brøk, fordi nævnerne er de samme.

Trin 6. Skriv de to nye fraktioner i rækkefølge
På dette tidspunkt har vi ikke tilføjet de to fraktioner sammen, selvom vi kan. I ovenstående trin multiplicerede vi hver brøk med 1. Nu vil vi sikre os, at de brøker, vi vil tilføje, har den samme nævner.
-
Opgave 3:
i stedet for 1/3 + 3/5 bliver brøkdelen 5/15 + 9/15
-
Opgave 4:
I stedet for 2/7 + 2/14 bliver brøkdelen 4/14 + 2/14

Trin 7. Tilføj tællerne for de to brøker sammen
Tælleren er tallet over kvotienten.
-
Opgave 3:
5 + 9 = 14. 14 er den nye tæller.
-
Opgave 4:
4 + 2 = 6. 6 er den nye tæller.

Trin 8. Skriv fællesnævner (i trin 2) under den nye tæller eller brug nævneren for brøken ganget med 1 for at udligne nævneren
-
Opgave 3:
15 er den nye nævner.
-
Opgave 4:
14 er den nye nævner.

Trin 9. Skriv en ny tæller og en ny nævner
-
Opgave 3:
14/15 er svaret 1/3 + 3/5 =?
-
Opgave 4:
6/14 er svaret 2/7 + 2/14 =?

Trin 10. Forenkle og reducere brøker
For at forenkle brøker skal du dividere tælleren og nævneren med den største fælles faktor for de to tal.
-
Opgave 3:
14/15 kan ikke forenkles.
-
Opgave 4:
6/14 kan reduceres til 3/7 efter dividering af tæller og nævner med 2 som den største fælles faktor på 6 og 14.
Tips
- Inden du tilføjer brøker, skal du kontrollere, at nævnerne er de samme.
- Saml ikke nævnerne. Hvis nævnerne er de samme, skal du bruge tallet som nævner, efter at brøkerne er tilføjet.
- Hvis du vil tilføje brøker med tal, der består af hele tal og brøker, skal du konvertere disse tal til brøker og tilføje dem i henhold til instruktionerne ovenfor.







