Det kan lyde skræmmende at finde antallet af udtryk i en aritmetisk serie, men det er faktisk ret simpelt. Du skal bare indtaste tallene i formlen U = a + (n - 1) b og find værdien af n, som er antallet af udtryk. Ved, at U er det sidste tal i serien, a er det første udtryk i serien, og b er forskellen mellem tilstødende termer.
Trin

Trin 1. Identificer det første, andet og sidste udtryk i serien
Normalt giver spørgsmål som dette de første 3 eller flere udtryk og det sidste udtryk.
Antag for eksempel, at dit spørgsmål er sådan: 107, 101, 95 … -61. I dette tilfælde er det første udtryk 107, og det sidste udtryk er -61. Du har brug for alle disse oplysninger for at løse problemet
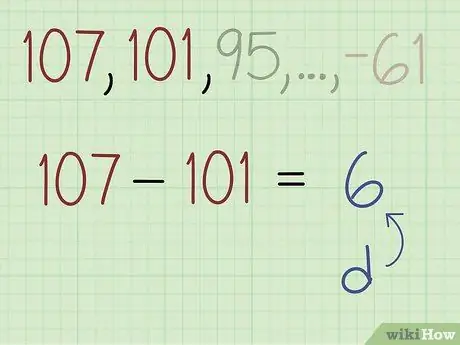
Trin 2. Træk det andet udtryk fra det første udtryk for at finde forskellen (b)
I eksempelproblemet er det første udtryk 107 og det andet udtryk er 101. For at finde forskellen trækker du 101 med 107 og får -6.
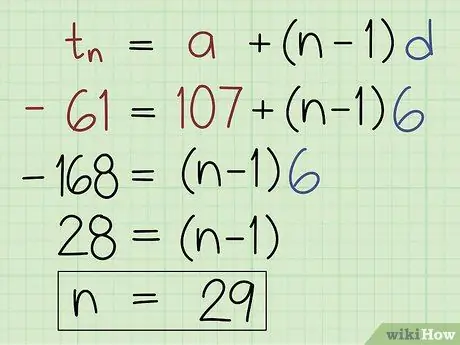
Trin 3. Brug formlen U = a + (n - 1) b for at finde n.
Indtast det sidste udtryk (U ), det første udtryk (a) og forskellen (b). Tæl ligningerne, indtil du får værdien af n.







