Hastighed er en beregning af, hvor hurtigt noget bevæger sig ad gangen. Hvis du nogensinde har set på speedometeret i en bil i bevægelse, vil du se hastigheden tælle - jo længere nålen kører, jo højere er køretøjets hastighed. Der er flere måder at beregne hastighed på, afhængigt af hvilken type information du har. Generelt formlen hastighed = afstand/tid (eller k = j/w) er den nemmeste måde at beregne hastighed på.
Trin
Metode 1 af 3: Brug af standardhastighedsberegningsformler

Trin 1. Find den afstand, et objekt har tilbagelagt
Den grundlæggende formel, som de fleste mennesker bruger til at finde hastigheden på noget, er meget let at bruge. Først og fremmest skal du vide "hvor lang afstand har det målte objekt tilbagelagt". Med andre ord, hvad er afstanden mellem objektets startpunkt og slutpunkt?
Denne formel er lettere at forstå gennem et eksempel. Lad os sige, at vi rejser i bil til en legeplads i "161 kilometer". I et par trin kan vi bruge disse oplysninger til at fuldføre beregningen af formlen

Trin 2. Find den tid, det tager objektet at rejse den afstand
Den næste information, du har brug for, er, hvor lang tid det tager objektet at nå en bestemt afstand. Med andre ord, hvor lang tid tager det for objektet at flytte fra startpunktet til slutpunktet?
I dette eksempel, lad os sige, at objektet tager ca. to timer at komme til destinationen.

Trin 3. Opdel afstanden med den tid, det tager at finde objektets hastighed
Du behøver kun disse to oplysninger for at kende objektets hastighed. Afstanden til tiden er lig med objektets hastighed.
I dette eksempel er 161 kilometer/2 timer = 80,5 kilometer i timen.

Trin 4. Glem ikke den anvendte enhed
Det er meget vigtigt at bruge de korrekte enheder i dit svar (f.eks. Kilometer i timen osv.) Uden disse enheder er det meget svært for folk at forstå betydningen af dit svar. Du kan også miste point, hvis du bruger den forkerte enhed, når du udfører opgaver fra skolen.
Enheden for hastighed er afstandsenhed til tidsenhed. For eksempel, da vi måler afstand i kilometer og tid i timer, er de anvendte enheder kilometer/time (eller kilometer i timen).
Metode 2 af 3: Løsning af mere vanskelige beregninger

Trin 1. Find flere forskellige variabler for at løse problemet med afstand og tid
Når du forstår den grundlæggende formel for hastighed, kan du bruge den til at udføre andre beregninger end hastighed. For eksempel, hvis du først kun kender objektets hastighed og en anden variabel, kan du omarrangere formlen ovenfor for at finde de ukendte oplysninger.
-
Lad os f.eks. Sige, at vi ved, at et tog kører med 20 kilometer i timen i fire timer, men vi ved ikke, hvor langt det er gået. For at finde ud af det kan vi omarrangere formlen på følgende måde:
-
- hastighed = afstand/tid
- hastighed × tid = (afstand/tid) × tid
- hastighed × tid = afstand
- 20 km/time × 4 timer = afstand = 80 kilometer
-

Trin 2. Konverter de enheder, du bruger, efter behov
Nogle gange kan du beregne hastighed ved hjælp af en bestemt enhed, men skal konvertere den til en anden enhed. I dette tilfælde skal du bruge en konverteringsfaktor for at få svaret i henhold til de korrekte enheder. For at gøre dette skal du blot skrive forholdet mellem enhederne i brøkform og multiplicere. Når du multiplicerer, vendes brøken efter behov for at fjerne uønskede enheder. Denne metode er meget lettere end den lyder!
-
Lad os f.eks. Sige, at vi i eksemplet ovenfor har brug for svaret i miles i stedet for kilometer. En kilometer svarer til cirka 1,6 kilometer. Så vi kan foretage konverteringen som følger:
-
- 80 kilometer × 1,6 kilometer = 50 miles
-
- Husk, fordi kilometer vises nederst i brøken, fjerner det kilometer fra det forrige svar, så det endelige resultat bruger miles.
- Dette websted indeholder konverteringsfunktioner til de fleste af de almindeligt anvendte enheder.

Trin 3. Udskift variablen "distance" med afstandsformlen efter behov
Objekter bevæger sig ikke altid i en lige, glat sti. Hvis dette er sandt, kan du muligvis ikke blot indtaste en numerisk værdi som en afstandsenhed i standardhastighedsformlen. Det kan dog være nødvendigt at udskifte bogstavet j i formlen k = j/w med en formel, der ligner den tilbagelagte afstand af objektet.
-
Lad os f.eks. Sige, at et fly roterer gennem luften en afstand på 20 miles 5 gange. Flyet gennemførte runden på en halv time. I dette eksempel skal vi stadig finde den samlede afstand, flyet har tilbagelagt, før vi kan bestemme dets hastighed. Vi kan bruge formlen til at beregne afstanden omkring en cirkel (afstanden omkring den) i stedet for j i denne formel. Denne formel er omkreds = 2πr, hvor r = cirkelradius. Sådan løser du det:
-
- k = (2 × × r)/w
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 miles/time
-

Trin 4. Forstå, at k = j/w giver gennemsnitshastigheden
Den lette og enkle formel, vi bruger til at finde hastighed, har en ulempe. Den resulterende værdi er teknisk set gennemsnitshastigheden. Det betyder, at formlen antager, at det objekt, du måler, bruger den samme hastighed, som det bevæger sig. Som vi vil se nedenfor, vil det være meget vanskeligere at finde et objekts hastighed i et enkelt øjeblik.
For at illustrere denne forskel, forestil dig sidste gang du rejste i bil. Det er usandsynligt, at du rejser med samme hastighed, som du rejser. Dog starter du normalt din rejse med lav hastighed og gradvist øger din hastighed undervejs, stopper på grund af rødt lys, trafikpropper osv. Hvis du bruger standardhastighedsformlen til at finde hastighed under kørsel, kan ændringer til denne hastighed ikke registreres. Du får dog et svar, der viser gennemsnitshastigheden for alle de hastighedsforskelle, du rejser
Metode 3 af 3: Beregning af øjeblikkelig hastighed
Bemærk:
Dette afsnit bruger teknikker, der er mindre velkendte for mennesker, der aldrig har studeret beregning. Læs vores artikler om beregning for at få hjælp.
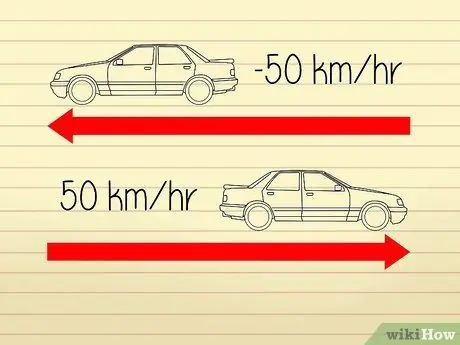
Trin 1. Forstå, at hastighed er defineret som accelerationshastigheden
Højhastighedsberegninger er ret forvirrende, fordi matematikere og forskere bruger forskellige definitioner til at beskrive "hastighed" og "acceleration". Acceleration har to komponenter: en "hastighed" og en "retning". Hastigheden er lig med objektets hastighed. En ændring i retning vil medføre en ændring i acceleration, men ikke en ændring i hastighed.
- Lad os f.eks. Sige, at to biler bevæger sig i modsatte retninger. Hastighedsmålere på begge biler viser et tal på 50 km/t, så de kører begge med samme hastighed. Men da bilerne bevæger sig væk fra hinanden, kan vi sige, at den ene bil har en "acceleration" på -50 km/t, mens den anden har en "acceleration" på 50 km/t.
- Ligesom øjeblikkelige hastighedsberegninger kan du også udføre øjeblikkelige accelerationsberegninger.

Trin 2. Brug absolutte værdier til at måle negativ acceleration
Et objekt kan have en negativ accelerationshastighed (hvis det bevæger sig i en negativ retning i forhold til et andet objekt). Der er dog ingen negativ hastighed. Så i dette tilfælde angiver hastighedens absolutte værdi objektets hastighed.
Derfor har begge biler i eksemplet ovenfor en hastighed på 50 km/t.
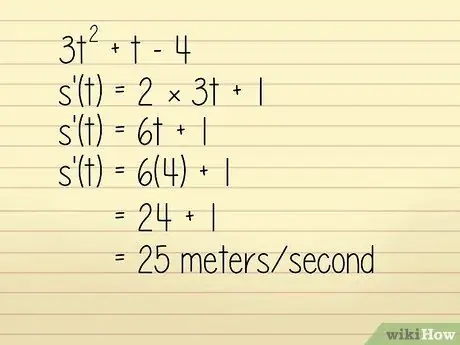
Trin 3. Tag afledningen af funktionens position
Hvis du har en funktion k (w), der viser et objekts position uden at skulle beregne tiden, viser derivatet af k (w) accelerationen uden behov for timing. Bare tilslut tidsværdien til denne formel, så variablen w (eller hvilken som helst tidsværdi der bruges) accelereres i henhold til den tid. Herfra kan du let finde objektets hastighed.
-
Lad os f.eks. Sige, at placeringen af et objekt i en meter er beskrevet i ligningen 3q2 + w - 4 hvor w = tid i sekunder. Vi vil gerne kende objektets hastighed ved w = 4 sekunder. I dette tilfælde kan du løse det ved at:
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Nu indtaster vi w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 meter/sekund. Teknisk set er dette en beregning af acceleration, men da den er positiv, og retningen ikke er nævnt i spørgsmålet, kan vi bruge den til at finde hastighed.
-

Trin 4. Tag den integrerede accelerationsfunktion
Acceleration er en måde at måle ændringen i et objekts acceleration over tid. Dette emne er for komplekst til at kunne forklares fuldstændigt i denne artikel. Det er imidlertid nyttigt at bemærke, at når du har en funktion a (w), der repræsenterer acceleration med hensyn til tid, vil integralet af a (w) returnere resultatet af acceleration baseret på den tid. Husk, det er meget nyttigt at kende den første acceleration af et objekt, så du kan definere konstanten for det resultat fra et uendeligt integralt.
-
Lad os f.eks. Sige, at et objekt har en konstant acceleration (i m/s2 som et resultat af a (w) = -30. Sig også, at objektet har en indledende acceleration på 10 m/s. Vi skal finde hastigheden ved w = 12 sekunder. I dette tilfælde kan vi løse det ved at:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
For at finde C løser vi p (w) for w = 0. Husk, at objektets oprindelige acceleration er 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, så p (w) = -30w + 10
-
-
Nu kan vi indtaste w = 12 sekunder.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Da hastighed er en absolut accelerationsværdi, er objektets hastighed 350 meter/sekund.
-
Tips
- Øvelse gør godt! Prøv at oprette dit eget spørgsmål ved at erstatte tallene i eksemplet ovenfor.
- Hvis du leder efter en hurtig måde at øve beregning på for bedre beregningshastighed, skal du bruge online -afledte lommeregner her og online integralberegner her.







