En matrix er et rektangulært arrangement af tal, symboler eller udtryk i rækker og kolonner. For at gange en matrix skal du gange elementerne (eller tallene) i matrixens første række med elementerne i matrixens anden række og lægge produktet sammen. Du kan multiplicere matricer med blot et par enkle trin, der kræver korrekt tilføjelse, multiplikation og placering af resultaterne.
Trin
Trin 1. Sørg for, at matricerne kan multipliceres
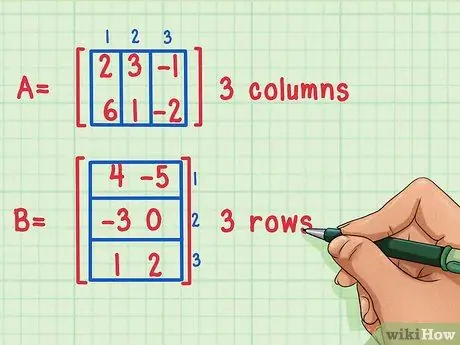
Du kan kun gange en matrix, hvis antallet af kolonner i den første matrix er lig med antallet af rækker i den anden matrix.
Disse matricer kan multipliceres, fordi den første matrix, Matrix A, har 3 kolonner, mens den anden matrix, Matrix B, har 3 rækker
Trin 2. Marker matrixproduktets dimensioner
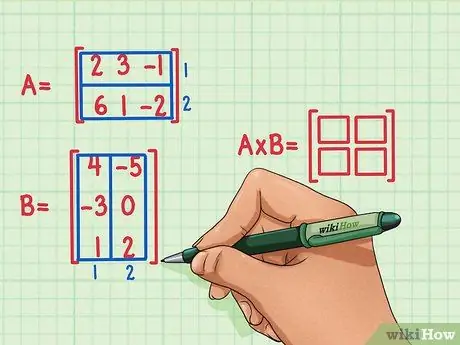
Opret en ny, tom matrix, som markerer dimensionerne af produktet af de to matricer. Matrixen, der repræsenterer produktet fra Matrix A og Matrix B, vil have det samme antal rækker som den første matrix og det samme antal kolonner som den anden matrix. Du kan tegne tomme felter for at vise antallet af rækker og kolonner i denne matrix.
- Matrix A har 2 rækker, så resultatet af multiplikation af matrixen vil have 2 rækker.
- Matrix B har 2 kolonner, så resultatet af multiplikation af matrixen vil have 2 kolonner.
- Resultatet af matrixproduktet vil have 2 rækker og 2 kolonner.
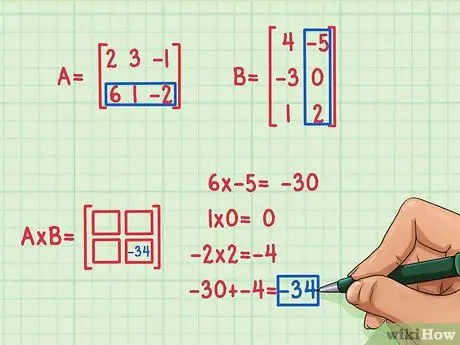
Trin 3. Find resultatet af det første prikprodukt
For at finde resultatet af det første prikprodukt skal du gange det første element i den første række med det første element i den første kolonne, det andet element i den første række med det andet element i den første kolonne og det tredje element i den første række ved det tredje element i den første kolonne. Tilføj derefter multiplikationsresultaterne for at finde prikprodukt (prik).
Antag, at du først har besluttet at beregne elementerne i anden række og anden kolonne (nederst til højre) i matrixproduktet. Sådan gør du det:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
Resultatet af prikproduktet er -34, og dette resultat er skrevet nederst til højre på matrixproduktet.
Når du multiplicerer en matrix, skrives prikproduktet i rækken af den første matrix og kolonnepositionen i den anden matrix. Når du f.eks. Kender prikproduktet fra den nederste række i Matrix A og den højre kolonne i Matrix B, skrives svaret -34 i den nederste række og højre kolonne i matrixproduktet
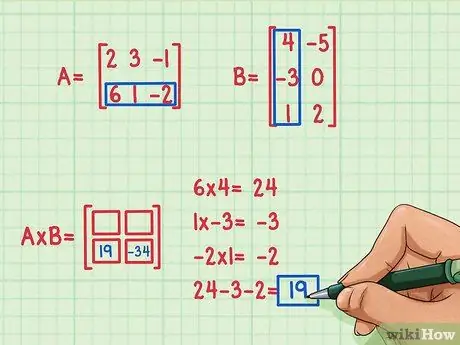
Trin 4. Find resultatet af det andet prikprodukt
Antag, at du vil finde udtrykket nederst til venstre på matrixproduktet. For at finde dette udtryk skal du blot gange elementerne i den nederste række i den første matrix med elementerne i den første kolonne i den anden matrix og derefter tilføje dem. Brug den samme metode som at gange den første række og kolonne - find igen prikprodukt (gør t)hans.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Resultatet af prikproduktet er -19, og dette resultat er skrevet nederst til venstre på matrixproduktet.
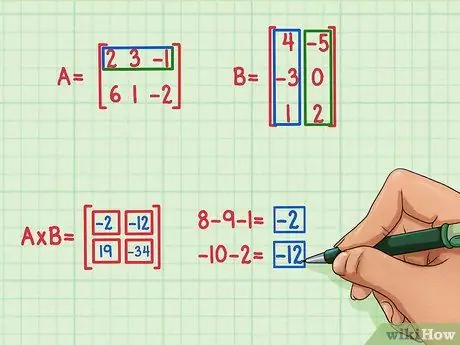
Trin 5. Find de to andre prikprodukter
For at finde udtrykket øverst til venstre i matrixproduktet skal du starte med at finde prikproduktet i den øverste række i Matrix A og venstre kolonne i Matrix B. Sådan gør du:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
Resultatet af prikproduktet er -2, og dette resultat er skrevet øverst til venstre på matrixproduktet.
For at finde udtrykket øverst til højre i matrixproduktet skal du bare kigge efter prikproduktet i den øverste række i Matrix A og den højre kolonne i Matrix B. Sådan gør du:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Punktproduktet er -12, og dette resultat er skrevet øverst til højre på matrixproduktet.
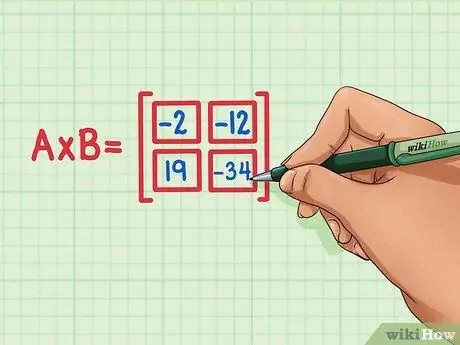
Trin 6. Sørg for, at de fire prikprodukter er på det rigtige sted i matrixproduktet
19 skal være nederst til venstre, -34 skal være nederst til højre, -2 skal være øverst til venstre, og -12 skal være øverst til højre.
Tips
- Brug af linjesegmenter og ikke brug af linjer kan give det forkerte svar. Hvis en linje, der repræsenterer en række, kræver en udvidelse for at krydse en kolonne, så forlæng den! Dette er blot en visualiseringsteknik for at gøre det lettere for dig at vide, hvilke rækker og kolonner der skal bruges til at arbejde med hvert element i produktet.
- Produktet af de to matricer producerer antallet af rækker svarende til antallet af rækker i den første matrix og antallet af kolonner, der er lig med antallet af kolonner i den anden matrix.
- Skriv din sum ned. Multiplikation af matricer indebærer en masse beregninger, og det er meget let at få sidesporet og glemme, hvilket tal du multiplicerer.







