Det er let at multiplicere brøker med blandede tal eller hele tal. Start med at konvertere blandede brøker eller hele tal til ukorrekte brøker (brøker med en større tæller end nævneren). Gang tælleren med de to brøker. Derefter multipliceres de to nævnere og forenkles produktet.
Trin
Metode 1 af 2: Multiplikation af to blandede fraktioner

Trin 1. Konverter blandede fraktioner til ukorrekte fraktioner
For at konvertere et blandet tal skal du multiplicere nævneren med et eksisterende heltal. Tilføj derefter en tæller til produktet. Placer det endelige resultat over linjen, og ændr ikke nævneren. Gentag dette trin for de andre blandede fraktioner.
Hvis du f.eks. Har et multiplikationsproblem på 1 1/2 x 4 4/7, skal du konvertere begge brøker til ukorrekte brøker. Fraktionen 1 1/2 kan ændres til 3/2 og 4 4/7 ændres til 32/7. Nu bliver dit multiplikationsproblem 3/2 x 32/7

Trin 2. Multiplicer tælleren for begge brøker
Når du har to ukorrekte brøker og ikke flere heltal i problemet, skal du gange de to tællere. Skriv resultatet og placer det over stregen.
- Tælleren er altid øverst i brøken.
- For eksempel, for problemet 3/2 x 32/7, multipliceres 3 med 32 for at få 96.

Trin 3. Multiplicer nævnerne for begge fraktioner
Multiplicer nu tallet under linjen og skriv resultatet under tælleren.
For eksempel, for problemet 3/2 x 32/7, gang 2 med 7 for at få 14

Trin 4. Konverter svar til blandede brøker, hvis det er muligt
Hvis tælleren for produktet er større end nævneren, skal du finde et tal, der producerer et tal, der tilnærmer tælleren, når det multipliceres med nævneren (dette tal fungerer som et heltal senere). Derefter placeres forskellen mellem nævneren med hele tallet og tælleren over nævneren for at få formen med blandet tal.
- For eksempel, hvis du får 96/14 som resultat af multiplikation, skal du finde det tal, der resulterer i en sum, der er tæt på 96, når det multipliceres med 14. Det tal er 6, og du får 12 som forskellen mellem 14 x 6 og 96. Placer 12 over nævneren (14).
- Normalt vil læreren bede dig om at skrive svaret i samme form som spørgsmålet. Hvis du får et blandet tal som et problem, skal du også konvertere svaret til et blandet tal.

Trin 5. Forenkle resultaterne yderligere, hvis det er muligt
Det er muligt, at du får både hele tal og brøker. Se på brøkerne, og kontroller, om de kan forenkles. For eksempel, hvis du har et resultat på 6 12/14, divider 12/14 med 2 for at forenkle det til 6/7.
I dette eksempelproblem vil dit endelige svar være 6 6/7
Metode 2 af 2: Multiplicer fraktioner med heltal
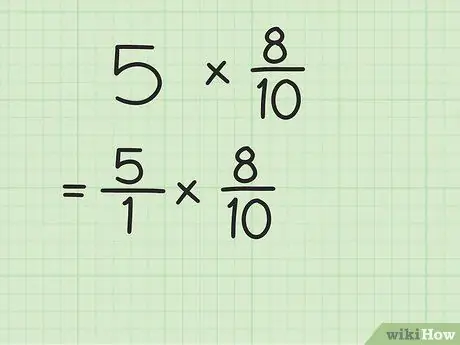
Trin 1. Omskriv hele tallet som en brøk
Hvis du vil omskrive et heltal som en brøkdel, skal du blot placere det over tallet 1 (nævneren). Herefter vil de eksisterende heltal blive til ukorrekte brøker.
For eksempel, hvis du har et problem med 5 x 8/10, skal du placere 5 over tallet 1. Nu er multiplikationen 5/1 x 8/10
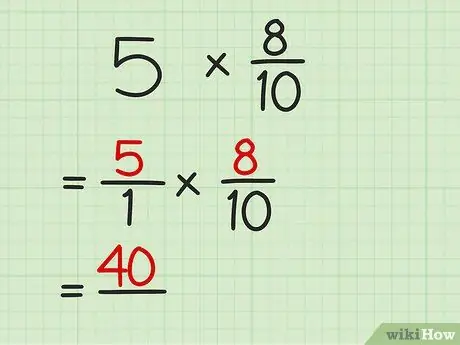
Trin 2. Multiplicer tælleren for begge brøker
Husk, at tælleren er det tal, der er over linjen. Skriv resultatet ned, og læg en linje under produktet.
For eksempel i 5/1 x 8/10 problemet, gang 5 med 8 for at få 40
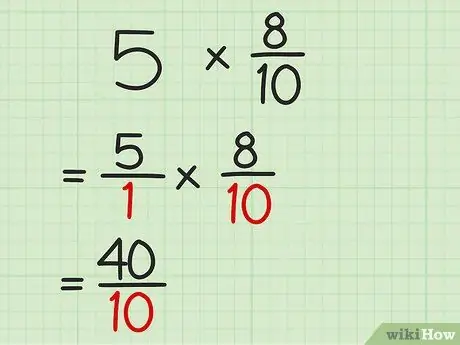
Trin 3. Multiplicer nævnerne for begge fraktioner
På dette tidspunkt kan du gange tallene under linjen for at få nævneren af produktet. Nu har du et multiplikationssvar i brøkform.
For eksempel, for et 5/1 x 8/10 problem, gang 1 med 10 for at få 10. Placer tallet under linjen, så produktet af de to brøker er 40/10
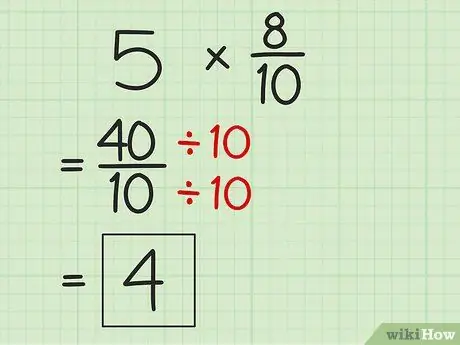
Trin 4. Skjul svar, hvis det er muligt
Da produktet af produktet kan være en ukorrekt fraktion, skal du forenkle resultatet til den mindste form. Divider tælleren med nævneren for at få et enklere resultat.
- For at forenkle 40/10 divideres 40 med 10 for at få 4 som det nye svar på multiplikationsproblemet.
- Normalt får du blandede tal, fordi resultatet af divisionen vil have en rest.







