P -værdien er en statistisk måling, der hjælper forskere med at afgøre, om deres hypotese er korrekt. P -værdien bruges til at bestemme, om resultaterne af deres eksperiment ligger inden for de værdier, der er normale for de undersøgte ting. Normalt, hvis P -værdien af et datasæt falder under en bestemt forudbestemt værdi (for eksempel 0,05), vil forskere afvise nulhypotesen i deres eksperiment - med andre ord vil de udelukke en hypotese, hvor den eksperimentelle variabel har ingen signifikant effekt. på resultatet. I dag findes p -værdier normalt i referencetabeller ved at beregne værdien for chi -kvadrat.
Trin

Trin 1. Bestem de forventede resultater af dit eksperiment
Normalt, når forskere foretager et eksperiment og undersøger resultaterne, har de allerede en idé om de normale eller almindelige resultater på forhånd. Dette kan baseres på resultaterne af tidligere forsøg, pålidelige observationsdatasæt, videnskabelig litteratur og/eller andre kilder. For dit eksperiment skal du bestemme dit forventede resultat og skrive det ned som et tal.
Eksempel: Antag, at en tidligere undersøgelse viste, at på nationalt plan blev der oftere udstedt hastighedsbilletter til røde biler end til blå biler. Antag, at gennemsnitsresultatet på nationalt niveau viser et forhold på 2: 1, hvor forholdet mellem røde biler er mere. Vi vil finde ud af, om politiet i vores by også får den samme tendens ved at analysere hastighedsbilletten udstedt af politiet i vores by. Hvis vi tog en stikprøve på 150 hastighedsbilletter givet til både røde og blå biler i vores by, ville vi forvente 100 til rød bil og 50 for blå biler, hvis politienheden i vores by giver en billet i henhold til sammenligningen på landsplan.

Trin 2. Bestem dine eksperimentelle observationer
Nu hvor du har bestemt din forventede værdi, kan du køre dit eksperiment og finde den sande værdi (eller observation). Igen, skriv resultatet ned som et tal. Hvis vi manipulerer nogle eksperimentelle forhold, og de observerede resultater adskiller sig fra de forventede resultater, findes der to muligheder: enten skete det tilfældigt, eller også var det vores manipulation af de eksperimentelle variabler, der forårsagede denne forskel. Formålet med at finde p-værdien er dybest set at afgøre, om de observerede resultater adskiller sig fra de forventede resultater til et punkt, hvor nulhypotesen-hypotesen om, at der ikke er noget forhold mellem den eksperimentelle variabel og de observerede resultater-ikke kan afvises.
Eksempel: Antag, at vi i vores by tilfældigt vælger 150 hastighedsbilletter, der tildeles både røde og blå biler. Vi får 90 en billet til en rød bil og 60 til den blå bil. Dette er forskelligt fra det resultat, vi forventede, dvs. 100 og 50. Har vores eksperimentelle manipulation (i dette tilfælde ændring af datakilden fra national til lokal) forårsaget nogen ændring i resultaterne, eller havde vores bypoliti de samme tendenser som det nationale niveau, og vi har lige observeret tilfældigheder? P -værdien hjælper os med at bestemme den.

Trin 3. Bestem frihedsgrader for dit eksperiment
Frihedsgraderne er et mål for mængden af variation i undersøgelsen, som bestemmes af antallet af kategorier, du undersøger. Ligningen for frihedsgrader er Frihedsgrader = n-1, hvor n er antallet af kategorier eller variabler, der er analyseret i dit eksperiment.
-
Eksempel: Vores eksperiment har to kategorier af resultater: en for den røde bil og en for den blå bil. Således har vi i vores eksperiment 2-1 = 1 frihedsgrad.
Hvis vi sammenligner røde, blå og grønne biler, vil vi have
Trin 2. frihedsgrader og så videre.

Trin 4. Sammenlign de forventede resultater med de observerede resultater ved hjælp af chi -kvadrat
Chi i firkant (skrevet x2) er en numerisk værdi, der måler forskellen mellem de forventede og observerede værdier fra eksperimentet. Ligningen for chi i firkant er: x2 = ((o-e)2/e), hvor o er den observerede værdi og e er den forventede værdi. Tilføj resultaterne af denne ligning for alle mulige resultater (se nedenfor).
- Bemærk, at denne ligning bruger operatoren (sigma). Med andre ord skal du beregne ((| o-e | -.05)2/e) for hvert muligt resultat, og tilføj derefter resultaterne for at få chi -kvadratværdien. I vores eksempel har vi to resultater - en bil, der får en rød eller en blå billet. Således kan vi beregne ((o-e)2/e) to gange - én gang for den røde bil og én gang for den blå bil.
-
Eksempel: Lad os tilslutte vores forventede værdier og observationer til ligningen x2 = ((o-e)2/e). Husk, at vi på grund af sigma-operatoren skal beregne ((o-e)2/e) to gange - én gang for den røde bil og én gang for den blå bil. Behandlingstrinnene er som følger:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Trin 5. Vælg et betydningsniveau
Nu hvor vi kender vores eksperimentelle kits frihedsgrader og chi-kvadratværdien, er der kun en sidste ting, vi skal gøre, før vi kan finde vores p-værdi-vi skal bestemme niveauet for betydning. Grundlæggende er signifikansniveau en måling af, hvor sikre vi er på vores resultater - et lavt niveau af betydning svarer til en lav sandsynlighed for, at resultatet af et eksperiment skyldtes tilfældigheder og omvendt. Signifikansniveauet skrives som en decimal (f.eks. 0,01), hvilket svarer til den procentvise chance for, at resultatet af forsøget skyldtes tilfældigheder (i dette tilfælde 1%).
- Efter konventionen satte forskere normalt en signifikansværdi for deres eksperimenter til 0,05 eller 5 procent. Det betyder, at eksperimentelle resultater, der svarer til dette niveau af betydning, højst har en 5% chance for tilfældighed. Med andre ord er der en 95% chance for, at resultaterne skyldes videnskabsmandens manipulation af de eksperimentelle variabler, og ikke tilfældighed. For de fleste forsøg anses 95% tillid til forholdet mellem de to variabler for at have haft succes med at demonstrere forholdet mellem de to.
- Eksempel: For vores røde og blå bileksempel, lad os følge den videnskabelige aftale og bestemme vores betydningsniveau på 0, 05.
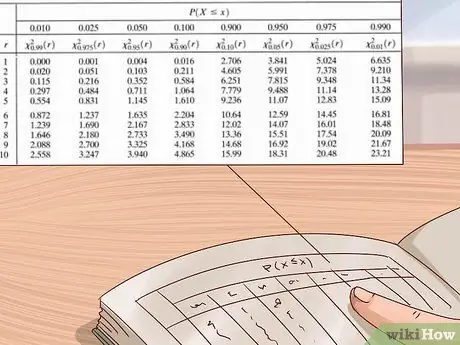
Trin 6. Brug chi square distributionstabellen til at estimere din p-værdi
Forskere og statistikere bruger store værditabeller til at beregne p -værdier for deres eksperimenter. Denne tabel er normalt skrevet med den lodrette akse til venstre, der viser frihedsgrader, og den vandrette akse øverst viser p-værdierne. Brug denne tabel ved først at finde dine frihedsgrader og derefter læse rækkerne fra venstre mod højre, indtil du finder den første værdi, der er større end din chi -kvadratiske værdi. Se på p-værdien øverst i kolonnen-din p-værdi er mellem denne værdi og den næststørste værdi (den rigtige værdi er til venstre for den).
- Chi -firkantede distributionstabeller er tilgængelige fra en række forskellige kilder - de kan let findes online eller i videnskabs- eller statistikbøger. Hvis du ikke har en, kan du bruge tabellen vist på billedet ovenfor eller et gratis online bord, f.eks. Det fra medcalc.org her.
-
Eksempel: Vores chi-kvadrat er 3. Så lad os bruge chi-kvadratfordelingstabellen på billedet ovenfor for at finde en omtrentlig p-værdi. Da vi ved, at vores eksperiment kun har
Trin 1. frihedsgrader, starter vi fra det øverste bord. Vi går fra venstre mod højre i denne række, indtil vi finder en værdi højere end
Trin 3. - vores chi -kvadratværdi. Den første værdi, vi finder, er 3,84. Når vi ser op i denne kolonne, ser vi, at den tilsvarende p-værdi er 0,05. Det betyder, at vores p-værdi er mellem 0,05 og 0,1 (næststørste p-værdi i tabellen).

Trin 7. Beslut, om du vil afvise eller forsvare din nulhypotese
Da du har fundet en omtrentlig p-værdi for dit eksperiment, kan du beslutte, om du vil afvise dit eksperiments nulhypotese eller ikke (som en påmindelse er dette hypotesen om, at den eksperimentelle variabel, du manipulerede, ikke havde nogen effekt på de resultater, du observerede). Hvis din p-værdi er lavere end din signifikansværdi, tillykke-du har bevist, at der er stor sandsynlighed for, at der er en sammenhæng mellem de variabler, du manipulerede, og dine observationer. Hvis din p-værdi er større end din signifikansværdi, kan du ikke med sikkerhed sige, at de resultater, du observerer, er et resultat af ren tilfældighed eller manipulation af dit eksperiment.
- Eksempel: Vores p-værdi er mellem 0,05 og 0,1. Det vil sige, at den ikke er mindre end 0,05, så desværre kan ikke afvise vores nulhypotese. Det betyder, at vi ikke når den minimumsgrænse på 95%, som vi har sat, så det kan siges, at politiet i vores by giver billetbilletter til røde og blå biler i et forhold, der er ganske anderledes end landsgennemsnittet.
- Med andre ord er der en 5-10% chance for, at vores observationer ikke er et resultat af en ændring i placering (analyse af vores by, og ikke hele delen), men er tilfældigheder. Da vi leder efter en sandsynlighed på mindre end 5%, kan vi ikke sige, at vi overbevist at politiet i vores by har en tendens til at billetføre røde biler - der er en lille, men statistisk meget forskellig mulighed for, at de ikke har denne tendens.
Tips
- En videnskabelig lommeregner vil gøre beregningerne meget lettere. Du kan også søge efter regnemaskiner online.
- Du kan beregne p-værdier ved hjælp af flere computerprogrammer, herunder almindeligt anvendt regnearkssoftware og mere specialiseret statistisk software.







