Så længe du kender målingen for de to andre vinkler, er det let at finde den tredje vinkel i en trekant. Du skal bare trække summen af de to vinkler med 180 grader. Der er dog også andre måder, du kan bruge til at finde den tredje vinkel på en trekant, hvis problemets form er lidt anderledes end normalt. Hvis du vil vide, hvordan du finder den tredje vinkel i en trekant, skal du følge vejledningen herunder.
Trin
Metode 1 af 3: Brug af målene for de to andre vinkler
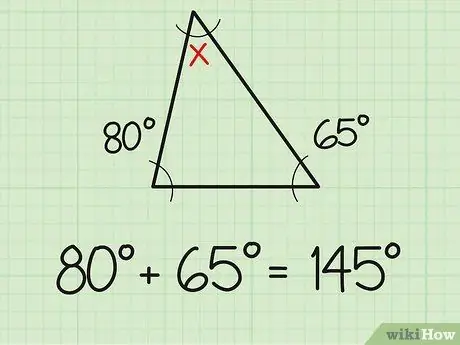
Trin 1. Tilføj de to kendte vinkler
Et faktum du bør vide er, at summen af de tre vinkler i en trekant altid er 180 grader. Så hvis du allerede kender målingen af de to vinkler i en trekant, er det lige så enkelt at finde den tredje vinkel som at lave simple additions- og subtraktionsproblemer. Saml først de to vinkelmål, du allerede kender. For eksempel måler to kendte vinkler 80 og 65 grader. Læg de to sammen (80+65), og du får 145 grader.
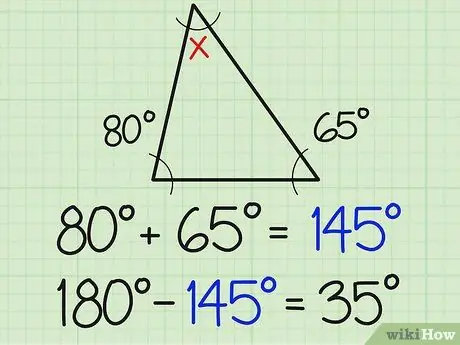
Trin 2. Divider dette tal med 180
Summen af de tre vinkler i en trekant er altid 180 grader. Derfor skal den tredje vinkel være 180, når den lægges til summen af de to kendte mål for vinklen. I eksemplet ovenfor betyder dette 180-154 = 35.

Trin 3. Skriv dit svar
Nu har du svaret på den tredje vinkel (i eksemplet 35 grader). Hvis du stadig er i tvivl, så se selv. Tilføj de tre vinkler sammen, og du skal få et resultat på 180. Hvis du ikke gør det, er din beregning forkert. I dette eksempel er 80+65+35 = 180. Hvis det er korrekt, betyder det, at du har løst problemet.
Metode 2 af 3: Brug af variabler
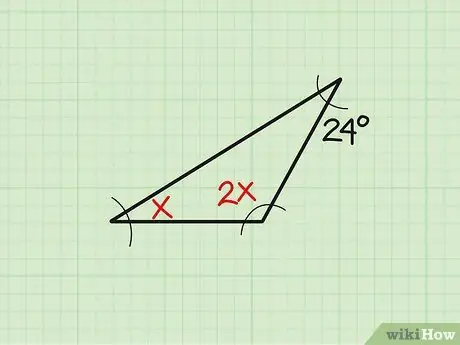
Trin 1. Skriv problemet op
Nogle gange vises størrelsen af den eksisterende vinkel i en variabel form. Lad os tage dette eksempel: "Find vinklen" x "i en trekant, hvis de tre vinkler måler henholdsvis" x "," 2x "og 24." Skriv først problemet ned.

Trin 2. Tilføj alle vinkelmålene
Det princip, du skal huske, er det samme. Så sammenlæg først de tre vinkler i problemet, nemlig "x+2x+24 = 3x+24".
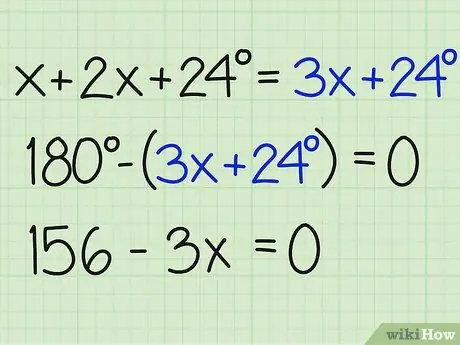
Trin 3. Del summen af vinklerne med 180
Nu, forskel dette tal med 180 grader for at finde x og finde ud af svaret på problemet. Sørg for at afslutte ligningen lig med nul. Sådan er det skrevet:
- 180- (3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
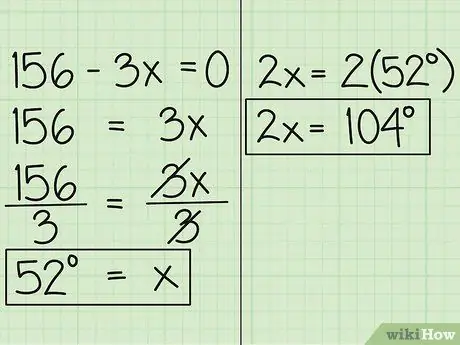
Trin 4. Find værdien af x
Flyt nu variablen til den anden side af ligningen, og du får 156 = 3x. Derefter divideres ligningen med 3, så du får x = 52. Det betyder, at målingen af vinklen udtrykt i x er 52 grader. Den anden vinkel, udtrykt i 2x er 52 grader gange 2, hvilket er 104 grader.

Trin 5. Kontroller dine resultater
Hvis du vil sikre dig, at dit svar er korrekt, skal du blot tilføje de tre vinkelmål, du allerede har fundet svaret på. Hvis resultatet er 180, betyder det, at dit svar er korrekt. I dette eksempel er 52+104+24 = 180.
Metode 3 af 3: Brug af andre metoder
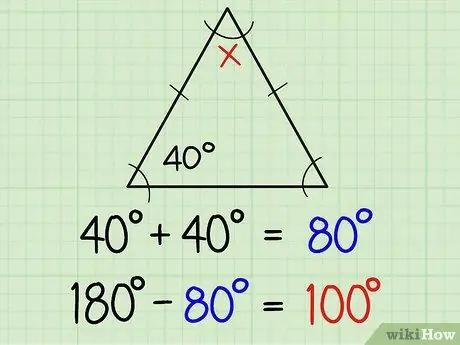
Trin 1. Find vinklerne på en ensartet trekant
En ensartet trekant har to lige store sider og to lige vinkler. To lige sider er normalt markeret med en lille linje midt på sidelinjen, hvilket betyder, at de to modsatte vinkler på linjen er det samme mål. Hvis du allerede kender størrelsen på den ene vinkel, kender du automatisk den anden vinkel. Her er yderligere forklaring:
Hvis en af de samme vinkler er 40 grader, så er den anden 40 grader. På den måde kan du finde alle tre vinkler med forskellen mellem summen af 40+40 (dvs. 80) og 180, eller med andre ord 180-80 = 100
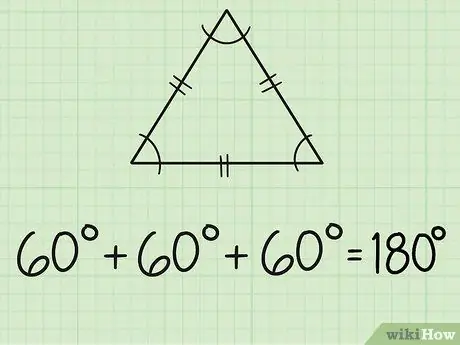
Trin 2. Find vinklerne på en ligesidet trekant
En ligesidet trekant har tre lige store sider og tre lige vinkler. Hver side er normalt markeret med to korte linjer i midten. Da alle tre vinkler er ens, betyder det, at alle vinklerne måler 60 grader, fordi 180/3 = 60.

Trin 3. Find den tredje vinkel i en højre trekant
Antag at du får en rigtig trekant, hvor en af de spidse vinkler måler 30 grader. Da trekanten er en ret vinkel, betyder det, at en af vinklerne, nemlig den rigtige vinkel, skal måle 90 grader. Brug derefter trekantsprincippet, forskellen mellem summen af de to vinkler (90+30 = 120) med 180, så får du 180-120 = 60 grader.







