Multiplicering af længder kan virke lidt skræmmende, især hvis du multiplicerer to tal, der er ret store. Men hvis du gør det trin for trin, vil du hurtigt kunne gennemføre lange multiplikationer. Gør dig klar til at fuldføre disse matematiske quizzer ved at se trin 1 nedenfor for at komme i gang.
Trin
Metode 1 af 2: Udførelse af almindelig lang multiplikation
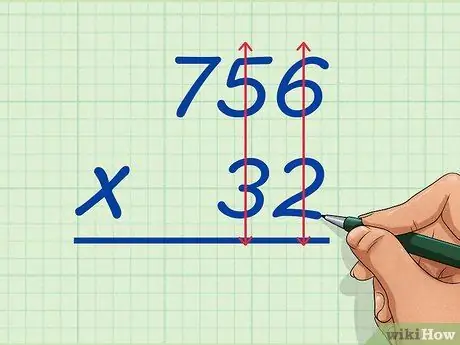
Trin 1. Skriv det store tal over det lille tal
For eksempel vil du gange 756 og 32. Skriv 756 over 32, og sørg for, at værdierne af en og tiere af de to tal stemmer overens, så 6 af 756 er over 2 af 32 og 5 af 756 er over 3 af 32 osv. Dette vil gøre det lettere for dig at forestille dig den lange multiplikationsproces.
Grundlæggende vil du begynde at gange 2 af 32 med alle 756 og derefter gange 3 af 32 med alle 756. Men gør det ikke endnu
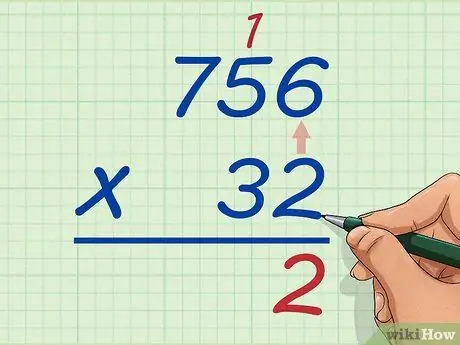
Trin 2. Multiplicér enhedens ciffer i det nederste tal med enhedscifret i det øverste nummer
Tag 2 af 32 og gang det med 6 af 756. Produktet af 6 og 2 er 12. Skriv enhedscifret, 2, under det ene sted, og flyt 1 over de 5. Grundlæggende skriver du, hvad produktet er i et sted, og hvis der er et tal på tierpladsen, skal du flytte det over tallet til venstre for det øverste tal, du lige har ganget. Du har 2 under 6 og 2.

Trin 3. Multiplicér dem cifret fra det nederste tal med ti -tallet fra det øverste tal
Multiplicer nu 2 og 5 med 10. Tilføj 1, du skrev over 5 til 10 for at gøre det til 11, og skriv derefter 1 ud for 2 i svarafsnittet. Du skal flytte tallet 1 på tierne over 7.

Trin 4. Multiplicér dem cifret fra det nederste tal med hundredvis fra det øverste tal
Nu multipliceres 2 med 7 til lige 14. Tilføj derefter den 1, du skrev ned til 14 for at få 15. Flyt ikke tierværdien, for der er ikke flere gangede tal for denne række. Skriv bare 15 i svarafsnittet.
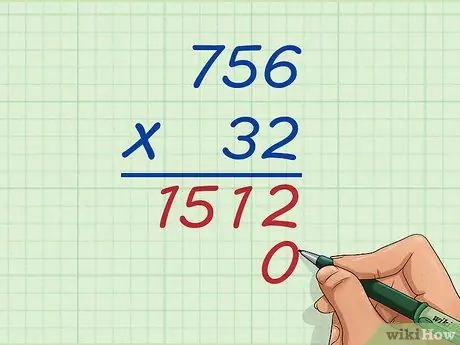
Trin 5. Skriv 0 i kolonnen enheder under det første multiplikationssvar
Nu vil du multiplicere ti -cifret med 32, hvilket er 3 med alle 756, så skriv et 0 under 2 på 1512, før du begynder at multiplicere, fordi du starter fra tier -stedet. Hvis du vil gange hundrederne med det øverste ciffer, skal du skrive to nuller ned og så videre.
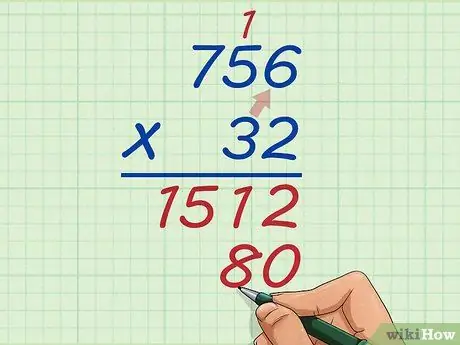
Trin 6. Gang ti -tallet fra det nederste tal med dem, der er cifret fra det øverste tal
Nu multipliceres 3 med 6 lig 18. Igen placeres de 8 ved siden af 0, og flyttes 1 over 5.

Trin 7. Multiplicer tiertallet fra bundnummeret med tiertallet fra det øverste tal
Gang 3 med 5. Resultatet er 15, men du skal tilføje det 1, der blev skrevet tidligere, så det bliver til 16. Skriv tallet 6 i svarafsnittet, og flyt tallet 1 over 7.

Trin 8. Multiplicer tiertallet fra det nederste tal med hundredvis fra det øverste tal
Multiplicere 3 med 7 er lig med 21. Tilføj tallet 1, der er skrevet tidligere for at gøre det 22. Du behøver ikke at flytte tiertallet 2 fra 22, fordi der ikke er flere tal, der kan multipliceres, så du kan bare skrive det ned næste til tallet 6.
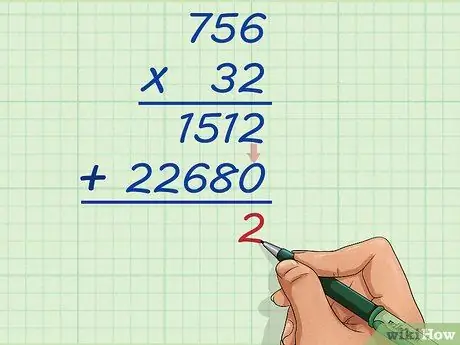
Trin 9. Tilføj enhedsværdierne for de to multiplikationsresultater
Nu skal du bare tilføje 1512 og 22680. Først tilføje 2 med 0 er lig 2. Skriv resultatet i kolonnen enheder.
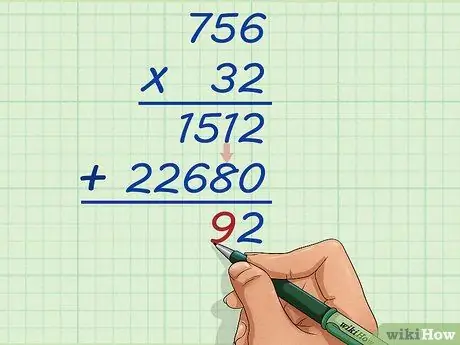
Trin 10. Tilføj de anden tiere af produktet
Nu, optælling af 1 og 8 er lig med 9. Skriv 9 til venstre for tallet 2.

Trin 11. Tilføj de andet hundredvis af multiplikationsresultater
Summen af 5 og 6 er 11. Skriv tallet 1 på stedet, og flyt tiertallet 1 over det 1, der er yderst til venstre for det første produkt.

Trin 12. Tilføj tusinder af de to multiplikationsresultater
Tilføj 1 med 2 er lig med 3, og tilføj derefter tallet 1, du skrev tidligere, så det bliver til 4. Skriv det ned.
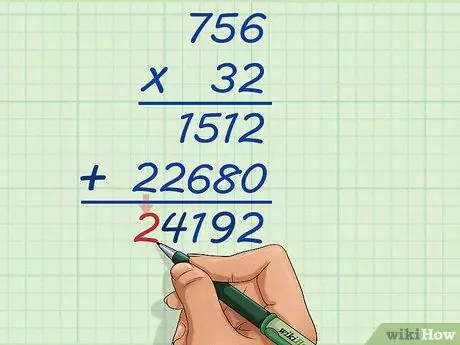
Trin 13. Tilføj titusinderne af de to multiplikationsresultater
Det første tal har ikke værdien af titusinder, og det andet tal har værdien 2. Så optæller 0 og 2 for at lave 2 og skriver det ned. Dit endelige svar vil være 24.192.

Trin 14. Kontroller dine svar ved hjælp af en lommeregner
Hvis du vil tjekke dit arbejde igen, skal du bruge en lommeregner til at kontrollere dine svar. Angiveligt er 756 gange 32 lig med 24.192. Du er færdig med det!
Metode 2 af 2: Forkort multiplikation

Trin 1. Skriv problemet ned
Antag, at du vil gange 325 med 12. Skriv det ned. Et tal skal være til højre for det andet nummer, ikke under det.
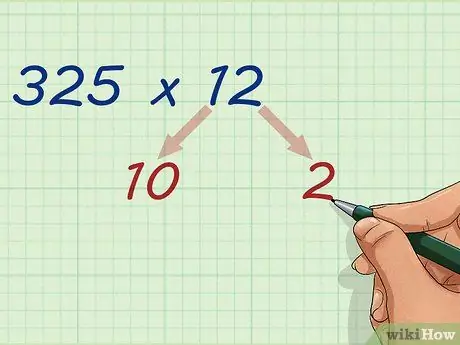
Trin 2. Opdel det mindre tal i tiere og enere
Lad tallet 325 være i fred, og del 12 i 10 og 2. 1 er på tierpladsen, så du skal altid tilføje 0 efter opdeling, og da 2 er det ene sted, kan du bare skrive tallet 2 ned.

Trin 3. Multiplicer det store tal med tallet på tierne
Nu ganges 325 med 10. Alt du skal gøre er at tilføje et nul i slutningen, så resultatet er 3250.

Trin 4. Gang det store tal med tallet på stedet
Nu ganges 325 med 2. Du kan forestille dig det og få 650, fordi 300 gange 2 er lig med 600 og 25 gange 2 er lig med 50. Tilføj 600 og 50 for at lave 650.
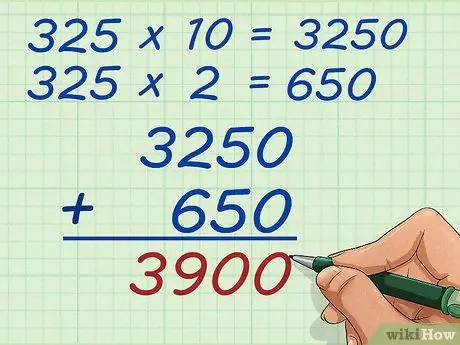
Trin 5. Tilføj de to produkter sammen
Nu skal du blot tilføje 3250 og 650. Du kan tilføje dem ved hjælp af den gammeldags tilføjelsesmetode. Skriv 3250 over 650 og foretag tilføjelsen. Du får 3.900 resultater. Dette er det samme som den almindelige lange multiplikationsmetode, men ved at opdele et tal i tiere og ens værdier kan du visualisere det og undgå at multiplicere og flytte tal for meget. Uanset hvad vil det give det samme resultat, og det er op til dig, hvilken vej der er hurtigere for dig.
Tips
- Træn først med korte, lette tal.
- Sørg for at indtaste dine tal i den korrekte kolonne!
- Glem ikke at flytte din ti -værdi, ellers bliver resultatet forkert.
- Sæt altid et 0 for enden af tierne. I hundredvis sætter TO 0'er og så videre. Kontroller også dit arbejde omhyggeligt, og brug en lommeregner til at kontrollere - men brug ikke en lommeregner til at beregne svar.
- For tal med mere end 2 cifre skal du følge disse trin: Først multiplicerer tallet ovenfor med enhederne, tilføjer derefter nul og multiplicerer med tiere, tilføjer derefter to nuller og multiplicerer med hundredvis, tilføjer derefter tre nuller og multiplicerer med tusinder og så videre. Saml alle tallene.







