Matematik er svært. Det er let at glemme selv de grundlæggende begreber, når du forsøger at huske de mange forskellige principper og metoder. Her er to friske måder at forenkle brøker på.
Trin
Metode 1 af 4: Brug af den største fælles faktor

Trin 1. Skriv tæller- og nævnefaktorer ned
Faktorer er tal, som du kan gange for at få et andet tal. For eksempel er 3 og 4 faktorer på 12, fordi du kan gange dem sammen for at få 12. For at nedskrive faktorerne i et tal, skal du bare skrive alle de tal ned, der kan multipliceres for at få det tal, og er delelige af faktorerne.
-
Skriv faktorernes tal ned fra den mindste til den største, uden at glemme at inkludere faktor 1. Sådan skriver du for eksempel tælleren og nævneren til brøken 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Trin 2. Find den største fælles faktor (GCF) for tælleren og nævneren
GCF er det største tal, der jævnt kan dele to eller flere tal. Når du har skrevet alle faktorens faktorer ned, skal du bare finde det største tal, der er det samme i begge lister over faktorer.
-
24: 1, 2, 3, 4, 6,
Trin 8., 12, 24.
-
32: 1, 2, 4,
Trin 8., 16, 32.
-
GCF på 24 og 32 er 8, fordi 8 er det største tal, der jævnt kan dele 24 og 32.

Trin 3. Divider tælleren og brøkdelen med GCF
Nu hvor du har GCF, skal du blot dividere tælleren og nævneren med dette tal for at forenkle din brøkdel til sin enkleste form. Sådan gør du:
- 24/8 = 3
- 32/8 = 4
- Den simple brøk er 3/4.

Trin 4. Kontroller dit arbejde
Hvis du vil sikre dig, at du har forenklet brøken korrekt, skal du blot gange den nye tæller og nævner med deres GCF for at få den originale brøkdel tilbage. Sådan gør du:
- 3 * 8 = 24
- 4 * 8 = 32
-
Du er vendt tilbage til sin oprindelige form, som er 24/32.
Du kan også kontrollere brøken for at sikre, at den ikke kan forenkles yderligere. Da 3 er et primtal, kan det kun divideres med 1 og sig selv, og fire er ikke delelige med 3, så brøken kan ikke forenkles yderligere
Metode 2 af 4: Fortsæt med at dividere med små tal

Trin 1. Vælg et lille antal
Ved at bruge denne metode skal du kun vælge et lille tal, f.eks. 2, 3, 4, 5 eller 7, til at starte med. Se på brøkerne for at sikre, at hver del er delelig med det nummer, du har valgt. For eksempel, hvis du har en brøkdel 24/108, skal du ikke vælge 5, fordi de ikke kan deles med 5. Men hvis du har en brøkdel 25/60, er 5 det rigtige tal at bruge.
For brøkdelen 24/32 er 2 et godt tal. Da begge tal er lige tal, kan de deles med 2

Trin 2. Divider tælleren og nævneren for brøken med tallet
Den nye brøk vil bestå af en ny tæller og nævner, som du får efter at have delt toppen og bunden af brøken 24/32 med 2. Sådan gør du:
- 24/2 = 12
- 32/2 = 16
- Din nye brøkdel er 12/16.
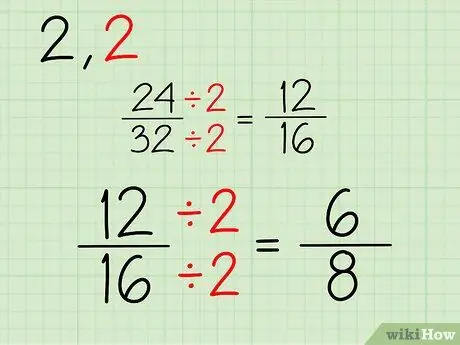
Trin 3. Gentag
Fortsæt denne proces. Da begge tal er lige tal, kan du blive ved med at dividere med 2. Hvis en eller begge tællere og nævnere er ulige tal, kan du prøve at dividere med et andet tal. Her er processen til at forenkle fraktionen 12/16:
- 12/2 = 6
- 16/2 = 8
- Din nye brøkdel er 6/8.

Trin 4. Bliv ved med at dele tallet, indtil det ikke længere er delbart
Den nye tæller og nævner er også lige tal, så du kan blive ved med at dividere med 2. Sådan gør du:
- 6/2 = 3
- 8/2 = 4
- Din nye brøkdel er 3/4.

Trin 5. Sørg for, at fraktionen ikke kan forenkles yderligere
I brøken 3/4 er 3 et primtal, så faktorerne er kun 1 og sig selv, og 4 er ikke delelig med 3, så brøken kan ikke forenkles yderligere. Hvis tælleren eller nævneren af brøken ikke længere kan divideres med det nummer, du har valgt, kan du stadig dele det med et andet tal.
For eksempel, hvis du har brøken 10/40, og du dividerer tælleren og nævneren med 5, er resultatet 2/8. Du kan ikke blive ved med at dividere tæller og brøk med 5, men du kan dele begge med 2, så slutresultatet er 1/4

Trin 6. Kontroller dit arbejde
Gang 3/4 med 2/2 igen tre gange for at sikre, at du får den første brøk, som er 24/32. Sådan gør du:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Bemærk, at du deler 24/32 med 2 * 2 * 2, hvilket er det samme som at dividere med 8, den største GCF på 24 og 32.
Metode 3 af 4: Skrivning af faktorerne

Trin 1. Skriv din brøkdel ned
Efterlad et stort mellemrum på højre side af dit papir - du skal bruge det til at skrive faktorerne ned.

Trin 2. Skriv faktorerne for tælleren og nævneren ned
Alene faktorerne for de to. Den nemmeste måde er, at faktorerne skrives oven på hinanden. Start med tallet 1, og skriv faktorerne ned.
-
For eksempel, hvis din brøkdel er 24/60, skal du starte med 24.
Skriv ned: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Derefter tallet 60.
Skriv ned: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Trin 3. Find og del med den største fælles faktor
Dette udtryk kan skrives som GCF i din trykte bog. Hvad er det største tal, der kan dele tæller og nævner? Uanset tallet, divider begge tal med dette tal.
For vores eksempel er det største tal, der er en faktor for begge tal, 12. Således deler vi 24 med 12 og 60 med 12, hvilket giver os 2/5 - vores simple brøk
Metode 4 af 4: Brug af et Prime Factor Tree

Trin 1. Find primærfaktorerne for tælleren og nævneren
Et primtal er et tal, der ikke kan divideres med et andet tal (bortset fra sig selv og 1, selvfølgelig). 2, 3, 5, 7 og 11 er eksempler på primtal.
- Start med tælleren. Fra 24, opdelt i 2 og 12. Da 2 allerede er et primtal, behøver du ikke at dividere det mere! Del derefter 12 i 2 tal: 2 og 6. 2 er primtal - fantastisk! Opdel nu 6 i 2 tal: 2 og 3. Du har nu 2, 2, 2 og 3 som dine primtal.
- Arbejd nu med nævneren. Fra 60 skal du dele dit træ i 2 og 30. 30 derefter opdele i 2 og 15. Derefter dele 15 i 3 og 5, som begge er primtal. Nu har du 2, 2, 3 og 5 som primtal.
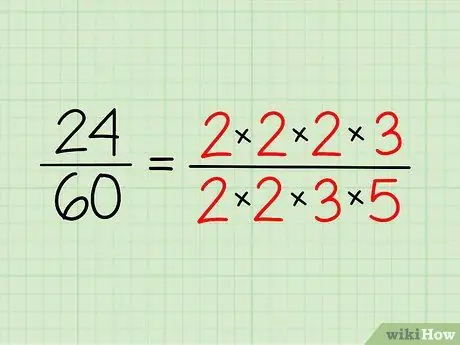
Trin 2. Skriv hovedfaktoriseringen af hvert tal ned
Skriv de primtal, du har for hvert tal, ned, og skriv dem i multiplikationsform. Du behøver ikke at gange det - det er bare en måde at gøre det lettere at se.
- Så for 24 har du 2 x 2 x 2 x 3 = 24.
- For 60 har du 2 x 2 x 3 x 5 = 60

Trin 3. Fjern de samme faktorer
Ethvert nummer, der er en del af begge numre, kan kasseres. I dette eksempel er de samme faktorer et par 2'ere og en 3. Farvel!
- Resten er 2 og 5 - eller 2/5! Det samme svar fik vi vejen ovenfor.
- Hvis brøkens tæller og nævner er lige tal, skal du ikke bare dividere med to. Fortsæt med at foretage opdelingen, indtil det nummer, du får, ikke kan deles igen.







