For de fleste mennesker er brøker de første komplicerede beregninger, man støder på. Begrebet fraktioner er ret svært og kræver, at du lærer særlige betingelser for at gøre det. Fordi brøker har særlige regler for addition, subtraktion, multiplikation og division, er mange mennesker forvirrede over det. Men med meget øvelse kan alle lære og færdiggøre beregninger relateret til brøker.
Trin
Metode 1 af 5: Forståelse af brøker
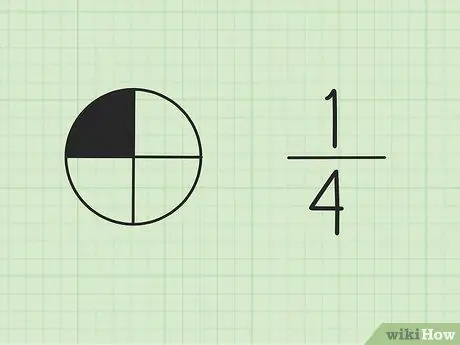
Trin 1. Forstå, at brøker er en del af en helhed
Tallet øverst kaldes tælleren og repræsenterer antallet af dele af totalen. Tallet nederst kaldes nævner, som repræsenterer det samlede antal dele.
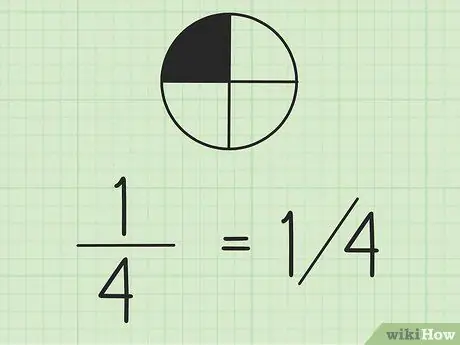
Trin 2. Husk på, at du kan skrive brøker ved hjælp af skråstreger
Tallet til venstre er tælleren, og tallet til højre er nævneren. Hvis du arbejder med brøker på samme linje, er det en god idé at skrive tælleren over nævneren.
For eksempel, hvis du tager en af fire pizzaskiver, har du pizza. Hvis du har 7/3 pizzaer, betyder det, at du har to hele pizzaer plus 1 ud af 3 pizzaskiver
Metode 2 af 5: Forskel mellem blandede og simple fraktioner

Trin 1. Forstå, at blandede tal består af hele tal og brøker, f.eks. 2 1/3 eller 45 1/2
Normalt skal du konvertere blandede tal til en enklere form for at tilføje, trække, multiplicere eller dividere.

Trin 2. Skift det blandede tal ved at gange hele tallet med nævneren i brøken og derefter tilføje det med tælleren
Skriv resultatet som tælleren, mens nævneren ikke ændres.
For eksempel, for at konvertere 2 1/3 til en simpel brøk, gange 2 med 3, tilføj derefter 1 og få 7/3

Trin 3. Konverter simple brøker til blandede tal ved at dividere tælleren med nævneren
Hele resultatet af divisionen skrives som et heltal, og resten af divisionen skrives som tælleren af brøken. Nævneren ændrer sig ikke.
For eksempel at konvertere 7/3 til et blandet tal ved at dividere 7 med 3 for at få 2 med en rest på 1. Så det blandede tal er 2 1/3. Enkle brøker kan kun konverteres til blandede tal, hvis tælleren er større end nævneren
Metode 3 af 5: Addition og subtraktion af fraktioner
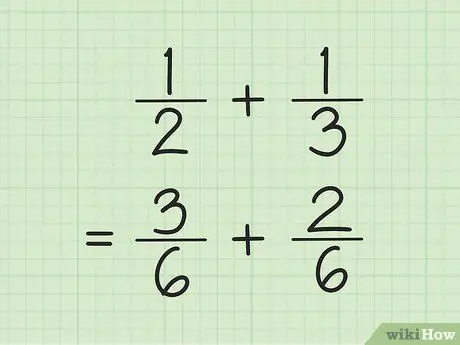
Trin 1. Find en fællesnævner for at tilføje og fratrække brøker
Tricket, gang tallene i nævneren, gang derefter hver tæller med det tal, der bruges til at finde nævneren. Nogle gange kan du finde LCM (mindst fælles multiplum) for nævneren ved at gange nævnerne med hinanden.
For eksempel, for at tilføje og 1/3, skal du først finde LCM (mindst fælles multiplum) for de to nævnere ved at gange hinanden. Således multiplicerer du 2 og 3 for at få LCM 6. Multiplicerer 1 med 3 for at få 3 som den nye tæller for den første brøk. Gang 1 med 2 for at få 2 som den nye tæller for den anden brøk. Dine nye brøker er 3/6 og 2/6
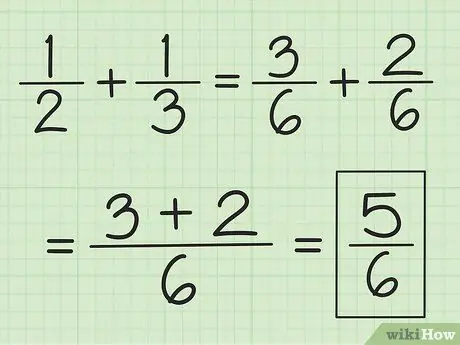
Trin 2. Tilføj de to tællere sammen, og skift ikke nævneren
For eksempel er 3/6 plus 2/6 5/6, og 2/6 plus 1/6 er 3/6
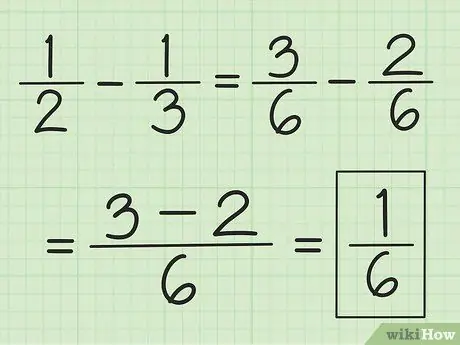
Trin 3. Brug en lignende teknik til subtraktion
Find LCM for nævnerne først, men i stedet for at lægge dem sammen, trækker du nummeret på den første tæller med nummeret på den anden.
For eksempel, for at trække 1/3 fra 1/2, skal du først ændre brøkerne til 3/6 og 2/6, derefter trække 3 med 2 for at få 1. Dette resulterer i 1/6
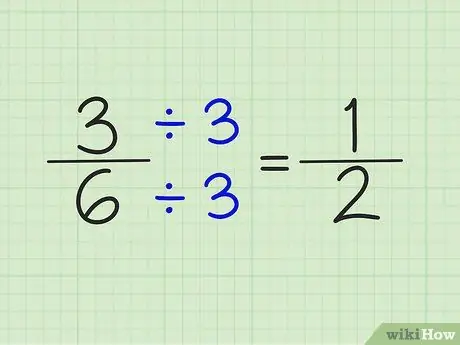
Trin 4. Forenkle brøker ved at dividere tælleren og nævneren med det samme tal
For eksempel kan tallet 5/6 ikke forenkles. 3/6 kan dog forenkles ved at dividere tælleren og nævneren med tallet 3. Resultatet er en brøkdel af 1/2

Trin 5. Konverter brøken til et blandet tal, hvis tælleren er større end nævneren
Metode 4 af 5: Multiplicer og del fraktioner
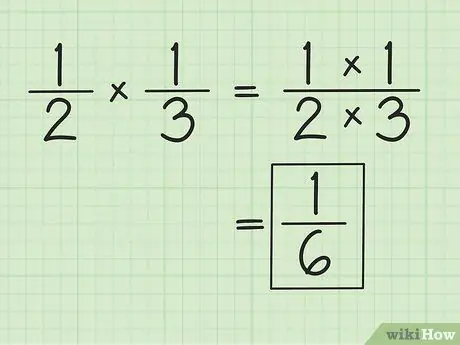
Trin 1. Multiplicer tælleren og nævneren separat for at multiplicere brøker
For eksempel, når man multiplicerer og 1/3, er resultatet 1/6 (1 gange 1 og 2 gange 3). Du behøver ikke at matche nævnerne, når du multiplicerer brøker. Forenkle eller ændre de opnåede resultater, hvis det er nødvendigt
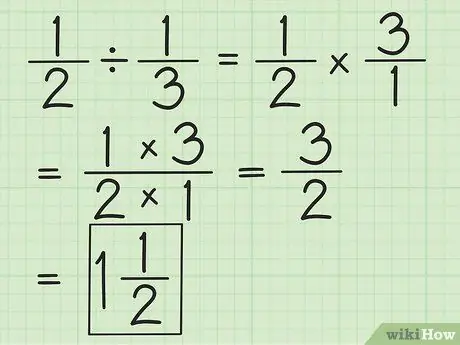
Trin 2. Del to brøker ved at vende den anden fraktion og derefter multiplicere begge
For eksempel, hvis du vil dividere 1/2 med 1/3, skal du først vende den anden brøk til 3/1. Gang med 3/1 og få 3/2. Forenkle brøker, eller konverter om muligt til blandede tal
Metode 5 af 5: Arbejde med komplekse fraktioner
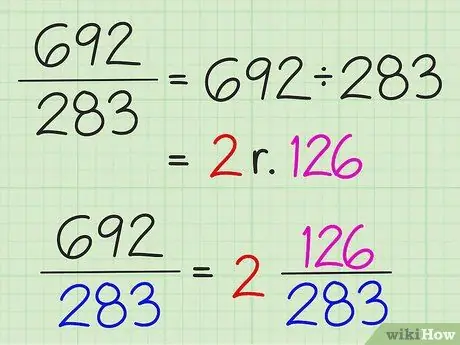
Trin 1. Arbejd alle brøkerne på samme måde, selvom problemet virker meget kompliceret
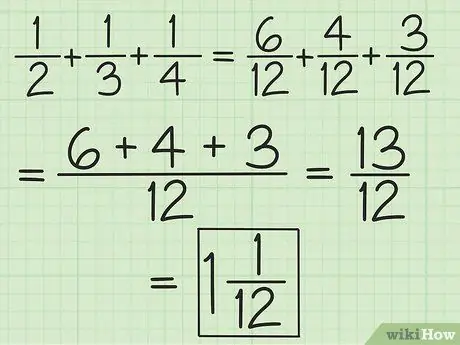
Trin 2. Match nævnerne for alle brøker eller arbejd parvis fra venstre mod højre for at tilføje og trække mere end to brøker
For eksempel, for at tilføje 1/2, 1/3 og 1/4, kan du ændre dem til 6/12, 4/12 og 3/12 for at få 13/12, eller du kan tilføje 3/6 og 2 /6 så du får 5/6, tilføj derefter 5/6 og 1/4 (udlign nævnerne, så den anden brøk bliver 3/12) for at få 13/12 (10/12 plus 3/12). Konverter det til et blandet tal, som er 1 1/12
Tips
- Husk, at du har lært ret meget matematik. Matematik er som et sprog, du kan udtale flydende, og nu prøver du at lære at læse og skrive det.
- Husk altid at forenkle det endelige resultat af din beregning, uanset om dit problem er i form af en almindelig brøk, et blandet tal eller en kompleks brøk.







