At tælle brøker er en af de mest nyttige matematiske færdigheder at udvikle. Inden du laver fraktionsberegninger, skal du lære at identificere dele og typer af brøker. Derefter kan du tilføje eller trække dem fra. For mere komplekse beregninger kan du lære at multiplicere og dividere brøker. Normalt skal du også forenkle eller reducere brøker.
Trin
Metode 1 af 4: Genkendelse af brøker

Trin 1. Find brøkdelen
Brøker skrives som et tal over skillelinjen og et andet tal under linjen.
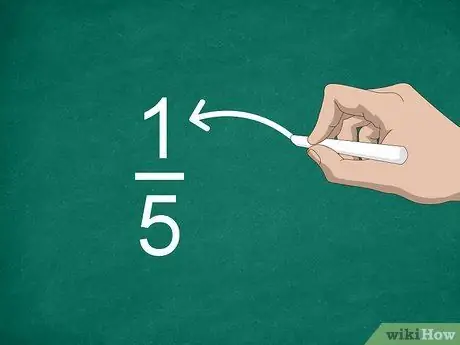
Trin 2. Identificer tælleren
Tallet over linjen kaldes tælleren og viser, hvor mange dele der er i brøken.
For eksempel i brøkdelen 1/5 er “1” tælleren
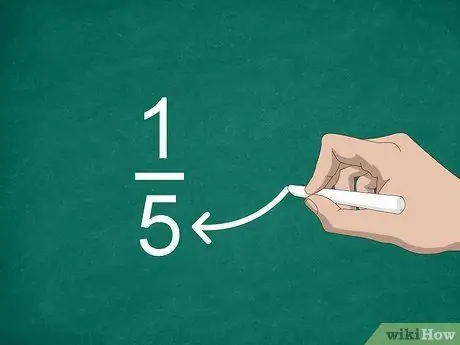
Trin 3. Find nævneren
Tallet placeret under linjen kaldes nævner. Denne værdi angiver antallet af dele, der "konstruerer" et helt tal.
For eksempel i brøkdelen 1/5 er "5" nævneren, så der er fem dele til fraktionen

Trin 4. Bestem om fraktionerne er rimelige fraktioner eller ukorrekte fraktioner
Hvis tælleren er mindre end nævneren, er brøken en naturlig brøk. I ukorrekte brøker er tælleren større end nævneren.
- For eksempel er 3/4 en rimelig brøkdel og 5/3 er en forkert brøk.
- Hvis du har et helt tal, der indeholder en brøk, er tallet kendt som et blandet tal. For eksempel er 1 1/2 et blandet tal.
Metode 2 af 4: Tilføj eller træk fraktioner fra

Trin 1. Identificer brøker med den samme nævner
Hvis du skal tilføje eller fratrække brøker, skal hver brøk have den samme nævner, før du udfører beregningen. Observer nævneren for hver brøkdel for at sikre, at de alle er ens (ens).
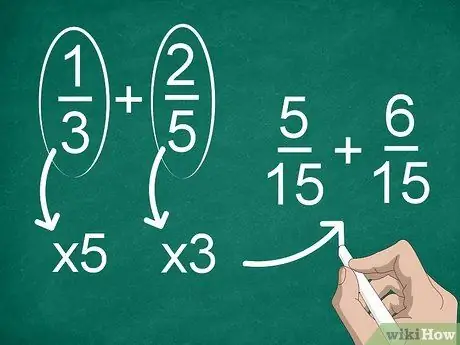
Trin 2. Find en fællesnævner, hvis hver brøkdel har en anden nævner
Hvis nævnerne ikke er de samme, skal du ændre brøkerne for at have den samme nævner. For at finde en fællesnævner ganges hver brøk med nævneren for den anden.
For eksempel, for at finde en fællesnævner i 1/3 + 2/5, skal du gange "1" og "3" med "5", derefter multiplicere "2" og "5" med "3". Nu har du tilføjelsen 5/15 + 6/15. Derefter kan du beregne brøkerne
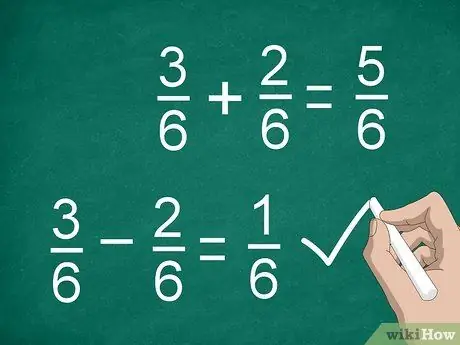
Trin 3. Tilføj eller træk tællerne til for at beregne brøker
Når du har fundet en fællesnævner og ganget tællerne (hvis det er nødvendigt), er du klar til at tilføje eller trække fra. Tilføj eller træk tællerne, og placer resultatet over skillelinjen. Skriv fællesnævneren under stregen.
- For eksempel 3/6 - 2/6 = 1/6.
- Tilføj eller træk ikke nævnerne.
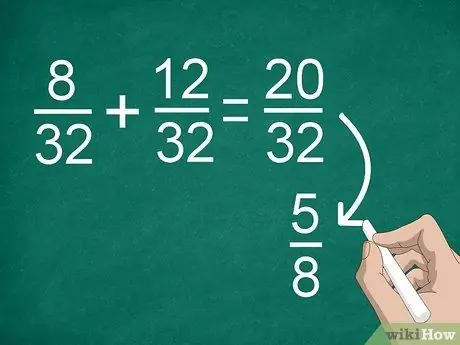
Trin 4. Forenkle resultaterne, hvis det er nødvendigt
Hvis du tidligere havde brug for at finde en fællesnævner, kan du få en stor brøkdel, som du kan forenkle. Hvis du f.eks. Tilføjer 8/32 +12/32, får du "20/32" som resultat. Denne brøkdel kan forenkles til “5/8”.
Metode 3 af 4: Multiplikation og forenkling af brøker
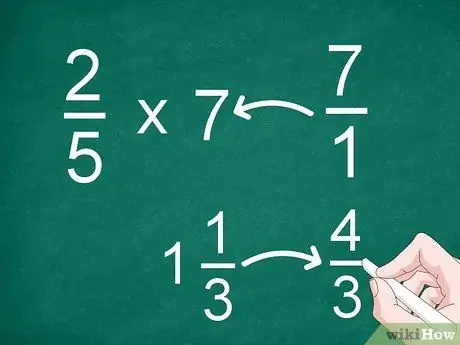
Trin 1. Konverter blandede brøker eller heltal til ukorrekte fraktioner
For at gøre multiplikation lettere skal du konvertere hvert tal til en rimelig eller forkert brøkdel. Hvis du har hele tal eller blandede tal, der skal multipliceres, skal du først konvertere dem til en almindelig brøk (naturlig eller forkert).
- For eksempel at multiplicere 2/5 med 7, konverter "7" til en brøk. Derefter kan du gange 2/5 med 7/1.
- Hvis du har et blandet tal som 1 1/3, skal du konvertere det til en forkert brøk ("4/3"), før du multiplicerer.
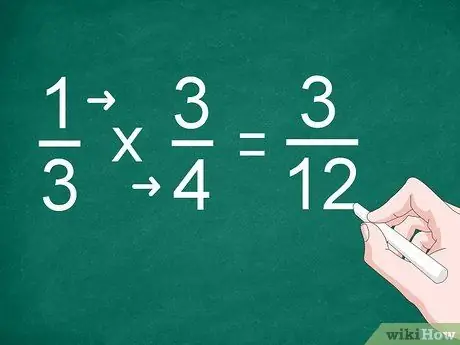
Trin 2. Multiplicer hver tæller og nævner
I stedet for at foretage tilføjelse skal du gange tælleren og skrive resultatet over skillelinjen. Du skal også multiplicere nævnerne og skrive resultatet under linjen.
For eksempel for at gange 1/3 med 3/4 skal du gange "1" med "3" for at få tælleren. Multiplicer "3" med "4" for at få nævneren. Svaret på multiplikationen er "3/12"

Trin 3. Forenkle resultaterne
Normalt skal du reducere resultatet til en enklere form, især hvis du i første omgang har unaturlige brøker. Find den største fælles faktor, og brug denne faktor til at forenkle tælleren og nævneren.
For brøkdelen 3/12 er den største fælles faktor mellem "3" og "12" for eksempel "3". Divider hvert element i brøken med "3", indtil du får brøkdelen "1/4"
Metode 4 af 4: Opdel fraktioner
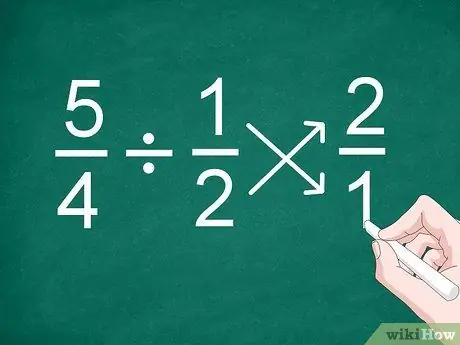
Trin 1. Vend placeringen af den anden fraktion
Den nemmeste måde at opdele brøker, selv brøker med forskellige nævnere, er at vende placeringen af den anden brøk, før du beregner resultatet.
For eksempel, for problemet 5/4 1/2, vendes positionen af brøken "1/2" for at blive "2/1"
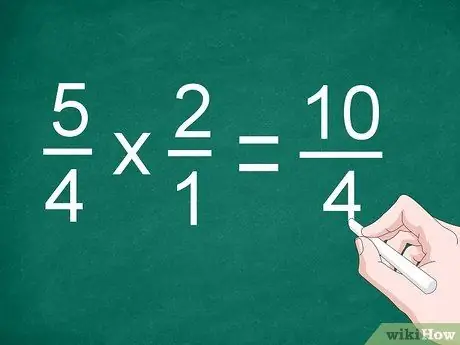
Trin 2. Multiplicer tælleren og nævneren
Multiplicer brøker direkte for at gange tællerne. Skriv resultatet over skillelinjen, og multiplicér derefter nævneren. Registrer produktet af nævnerne under linjen.
I det foregående eksempel multipliceres 5/4 med 2/1 for at få “10/4”
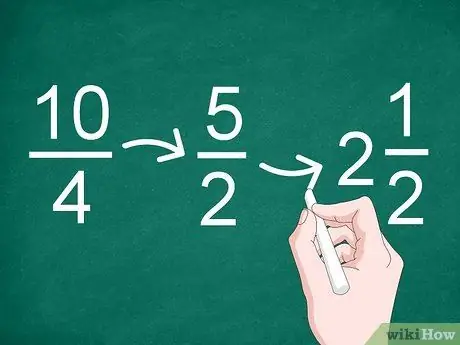
Trin 3. Forenkle resultaterne, hvis det er nødvendigt
Hvis resultatet af opdelingen er en ukorrekt brøkdel eller kan reduceres, skal du forenkle brøken. Brug den største fælles faktor til at reducere brøken.
- For eksempel er den største fælles faktor i brøkdelen 10/4 “2”, så resultatet af forenklingen bliver til “5/2” (10 divideret med 2 og 4 divideret med 2).
- Da resultatet af forenklingen er en forkert brøk, kan du konvertere det til et helt tal og en brøk (et blandet tal). Derfor kan 5/2 ændres til “2”.
Tips
- Hvis du arbejder med komplekse brøker, skal du tage nogle ekstra trin for at forenkle brøken. Denne forenkling i sig selv er imidlertid en obligatorisk del af beregningsprocessen.
- Skriv altid brøker pænt for at reducere risikoen for fejlberegninger.







